这篇文章描述2件事情:
1、已知球面上任意点,求过该点、地心、与北极点的平面方程(即过该点的经线平面方程);
2、绕过球心的任意轴旋转平面得到新平面的方程
一、已知球面上任意点,求过该点、地心、与北极点的平面方程(即过该点的经线平面方程)
输入经纬度,输出过该点,穿过地心、与北极点的平面方程,输出参数是平面方程的参数。
平面方程基本形式为:A*X+B*Y+C*Z+D=0
%% 已知球面上任意点,求过该点、地心、与北极点的平面方程(即过该点的经线平面方程)
%% 输入参数:任意点的经纬度(LNG,LAT)
%% 输出参数:平面方程的参数,平面方程的表达式为A*X+B*Y+C*Z+D=0
function [A,B,C,D]=GPS2EQPlane(LNG,LAT)
%% 地理常数
R=6371;%地球半径,单位km%% 经纬度转地理坐标系坐标
xt=R*cosd(LAT)*cosd(LNG);
yt=R*cosd(LAT)*sind(LNG);
zt=R*sind(LAT);%% 平面计算
% 计算单位法向量
nx = -yt/(sqrt(xt^2+yt^2));
ny = xt/(sqrt(xt^2+yt^2));
nz = 0;% 法向量
n = [nx; ny; nz];%% 求解平面方程的参数形式
A = n(1);
B = n(2);
C = n(3);
D = -(A * xt + B * yt + C * zt);
end二、绕过球心的任意轴旋转平面得到新平面
%% 绕过球心的任意轴旋转平面得到新平面
% 输入参数
% P:球面上的一点坐标,在直角坐标系下(x,y,z)
% N:原平面的法向量
% theta:绕旋转轴旋转的角度,单位度
% 输出参数:新平面的参数A*X+B*Y+C*Z+D=0
function [newA, newB, newC, newD] = rotatePlane(P, N, theta)
%% 地理常数
R=6371;%地球半径,单位km%% 计算点 P到球心的向量
OP = P; % 假设球心在原点,P 是点 P 的笛卡尔坐标
% 旋转轴的单位化
A = OP / norm(OP);%% 计算右乘旋转矩阵
C=cosd(theta);
S=sind(theta);
R=[C+A(1)^2*(1-C) A(1)*A(2)*(1-C)-A(3)*S A(1)*A(3)*(1-C)+A(2)*S;A(1)*A(2)*(1-C)+A(3)*S C+A(2)^2*(1-C) A(2)*A(3)*(1-C)-A(1)*S;A(1)*A(3)*(1-C)-A(2)*S A(2)*A(3)*(1-C)+A(1)*S C+A(3)^2*(1-C)];%% 旋转原平面的法向量
rotated_N = N*R;%% 计算新的平面方程的系数
newA = rotated_N(1);
newB = rotated_N(2);
newC = rotated_N(3);
newD = -(newA * P(1) + newB * P(2) + newC * P(3));
end三、示例
3.1 代码1示例
以海南凤凰机场为例:
三亚凤凰国际机场位于经度:109.414871、纬度:18.303421。
3.1.1 测试代码
clc;clear;close all
%% 经纬度和地理坐标系的转换仿真
%% 输入参数
R=6371;%地球半径,单位km
lng=109.414871;%经度
lat=18.303421;%纬度%% 算法计算
xt=R*cosd(lat)*cosd(lng);
yt=R*cosd(lat)*sind(lng);
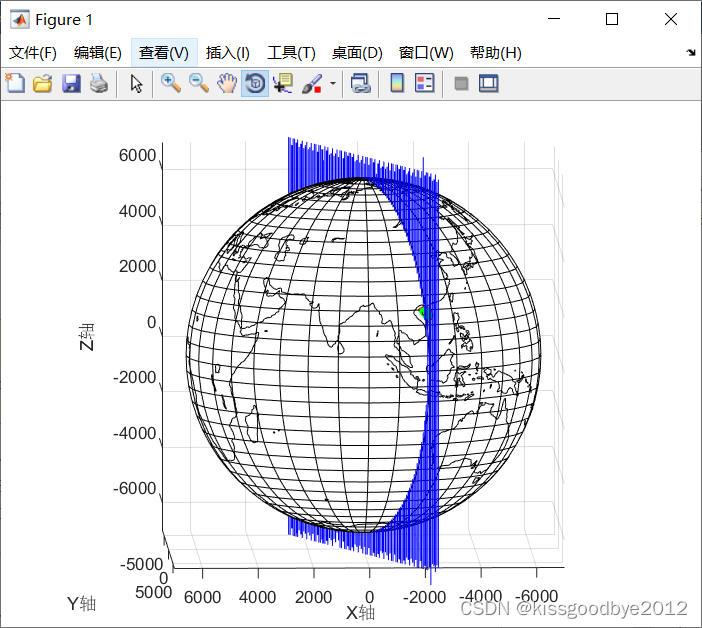
zt=R*sind(lat);%% 结果展示(绘制三维球体地图)
plot_Globe%% 结果展示(绘制三维点)
% 绘制三维点图
plot3(xt, yt, zt, 'o', 'MarkerSize', 10, 'MarkerEdgeColor', 'r', 'MarkerFaceColor', 'g');%% 平面计算
[A,B,C,D]=GPS2EQPlane(lng,lat);
%% 结果展示(绘制三维面)
plot_plane(A,B,C,D, 7000);% %% 旋转平面
% theta =90; % 旋转角度
% [newA, newB, newC, newD] = rotatePlane([xt yt zt],[A B C], theta);% %% 结果展示(绘制三维面)
% plot_plane(newA, newB, newC, newD, 7000);3.1.2 结果展示
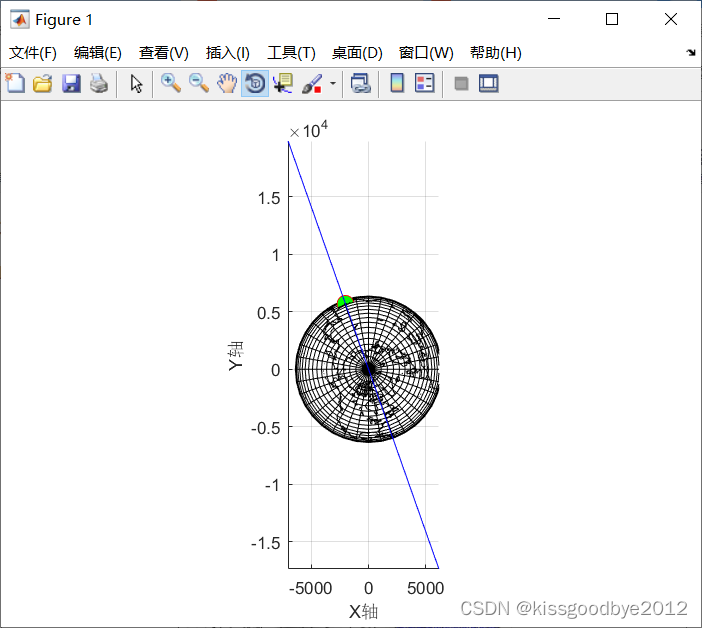
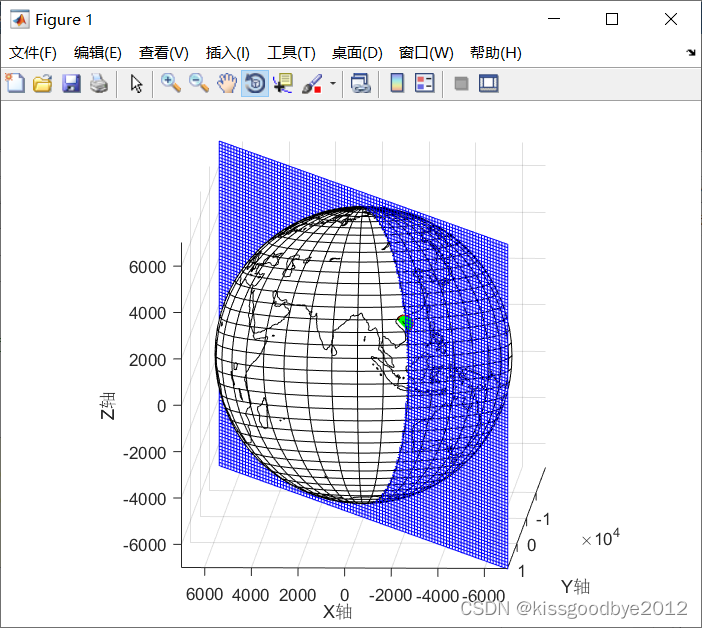
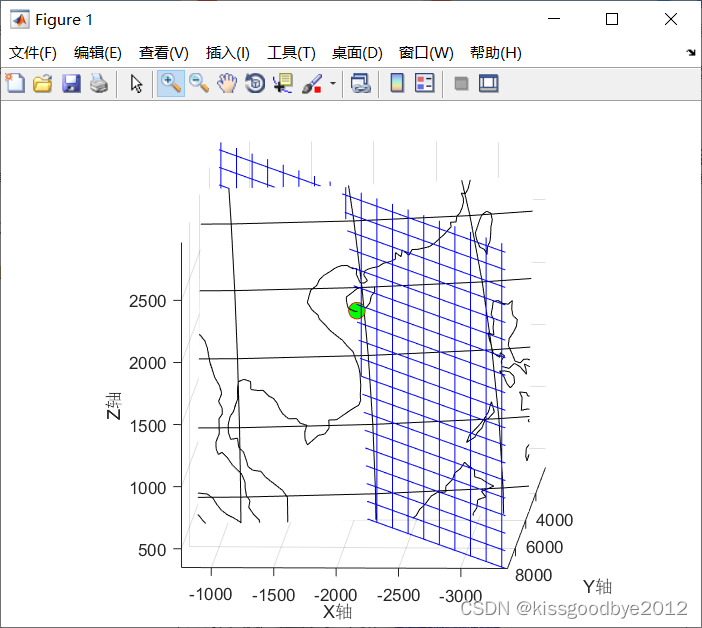
3.2 代码二示例
以经度:0、纬度:0为例:
3.1.1 测试代码
clc;clear;close all
%% 经纬度和地理坐标系的转换仿真
%% 输入参数
R=6371;%地球半径,单位km
lng=109.414871;%经度
lat=18.303421;%纬度%% 算法计算
xt=R*cosd(lat)*cosd(lng);
yt=R*cosd(lat)*sind(lng);
zt=R*sind(lat);%% 结果展示(绘制三维球体地图)
plot_Globe%% 结果展示(绘制三维点)
% 绘制三维点图
plot3(xt, yt, zt, 'o', 'MarkerSize', 10, 'MarkerEdgeColor', 'r', 'MarkerFaceColor', 'g');%% 平面计算
[A,B,C,D]=GPS2EQPlane(lng,lat);
% %% 结果展示(绘制三维面)
% plot_plane(A,B,C,D, 7000);%% 旋转平面
theta =45; % 旋转角度
[newA, newB, newC, newD] = rotatePlane([xt yt zt],[A B C], theta);%% 结果展示(绘制三维面)
plot_plane(newA, newB, newC, newD, 7000);3.1.2 结果展示
旋转45度后
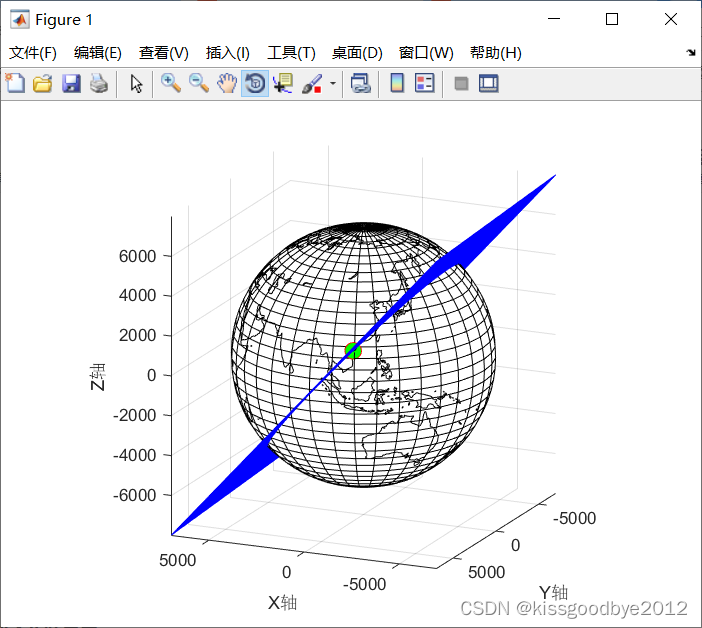
旋转90度后
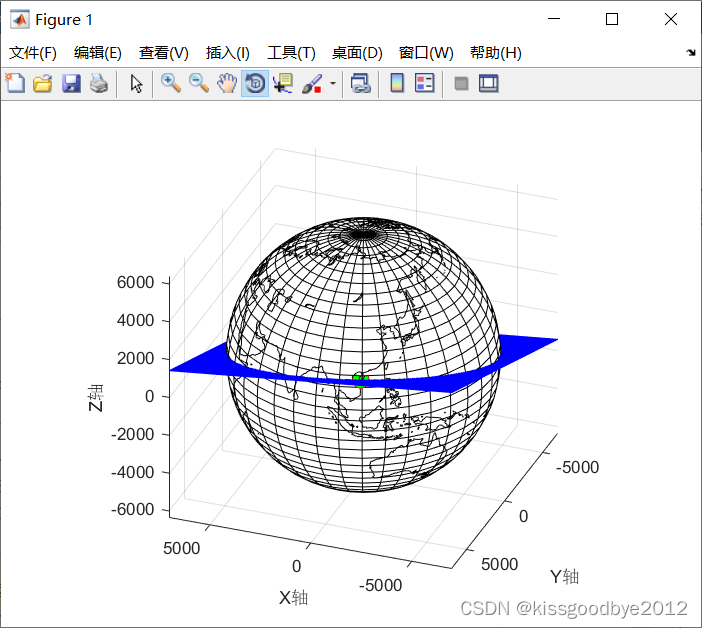
旋转180度后