Hive命令行客户端
Hive有两个主要的客户端工具,分别是旧版的Hive CLI(Command Line Interface)和新版的Beeline。
-
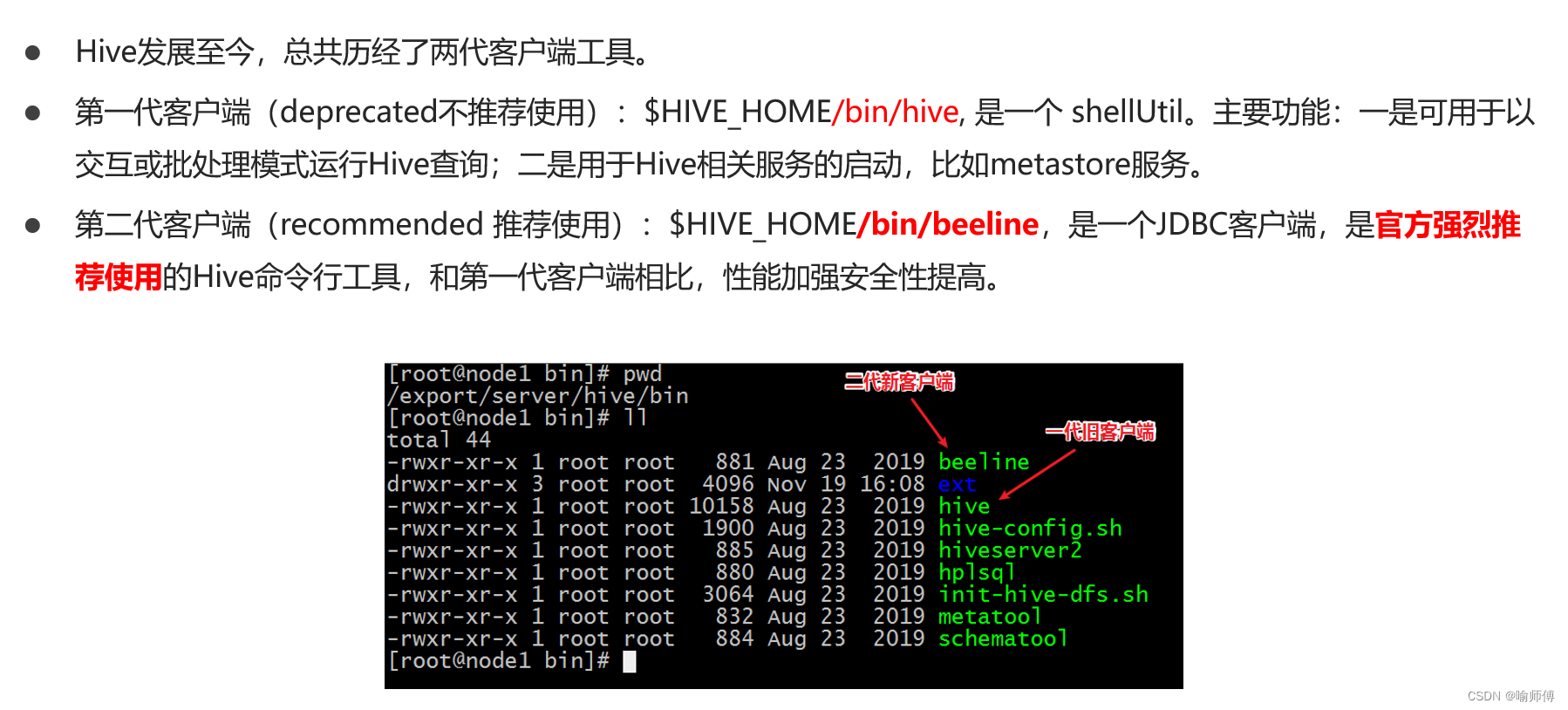
Hive CLI:
- Hive CLI 是 Hive 最早期的命令行客户端工具,它使用 JDBC 连接到 Hive 服务器,并提供了一个交互式的 shell 界面。在使用 Hive CLI 时,你可以直接在命令行中输入 HiveQL 查询,并查看执行结果。
- 优点:Hive CLI 的优点是简单易用,对于熟悉传统 Hive 开发的用户来说,操作起来比较熟悉。
- 缺点:Hive CLI 的缺点是性能相对较低,不支持一些新特性,而且在某些情况下不够稳定。因此,它已经逐渐被 Beeline 所取代。
-
Beeline:
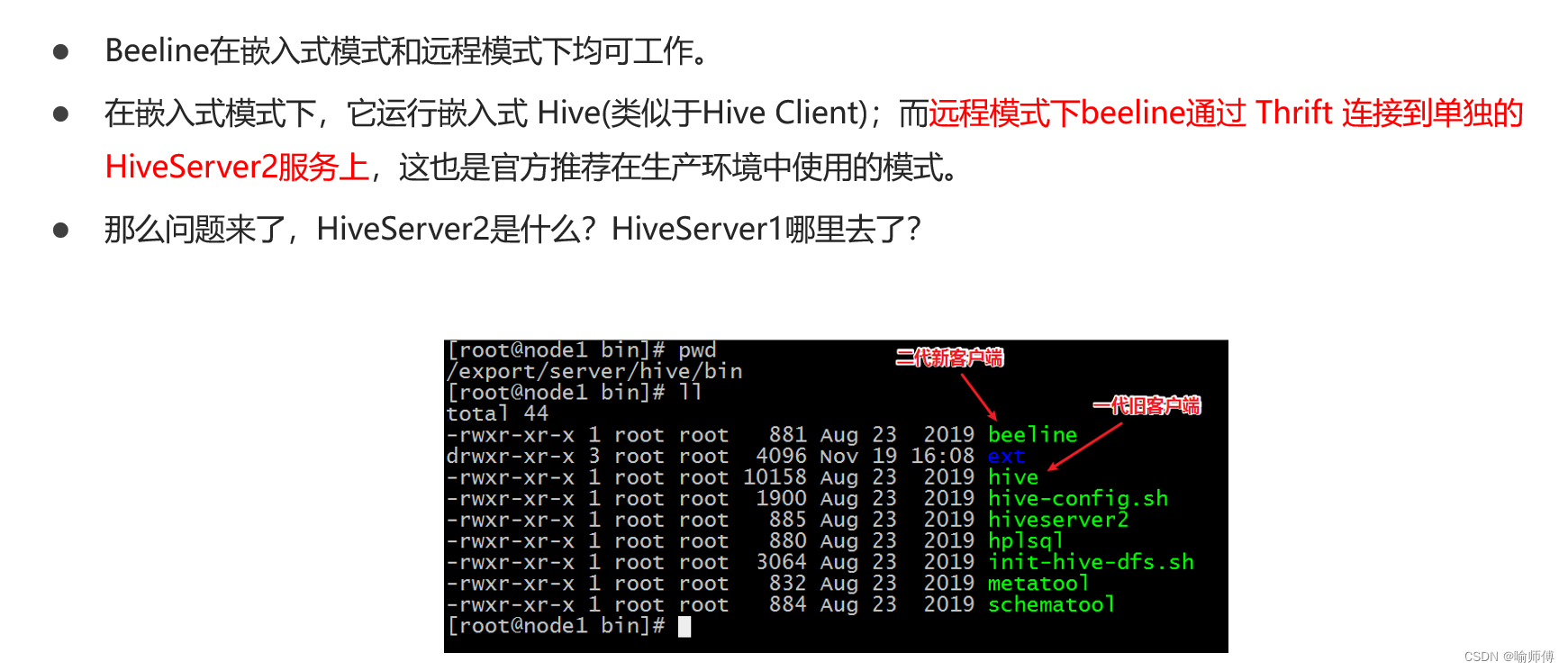
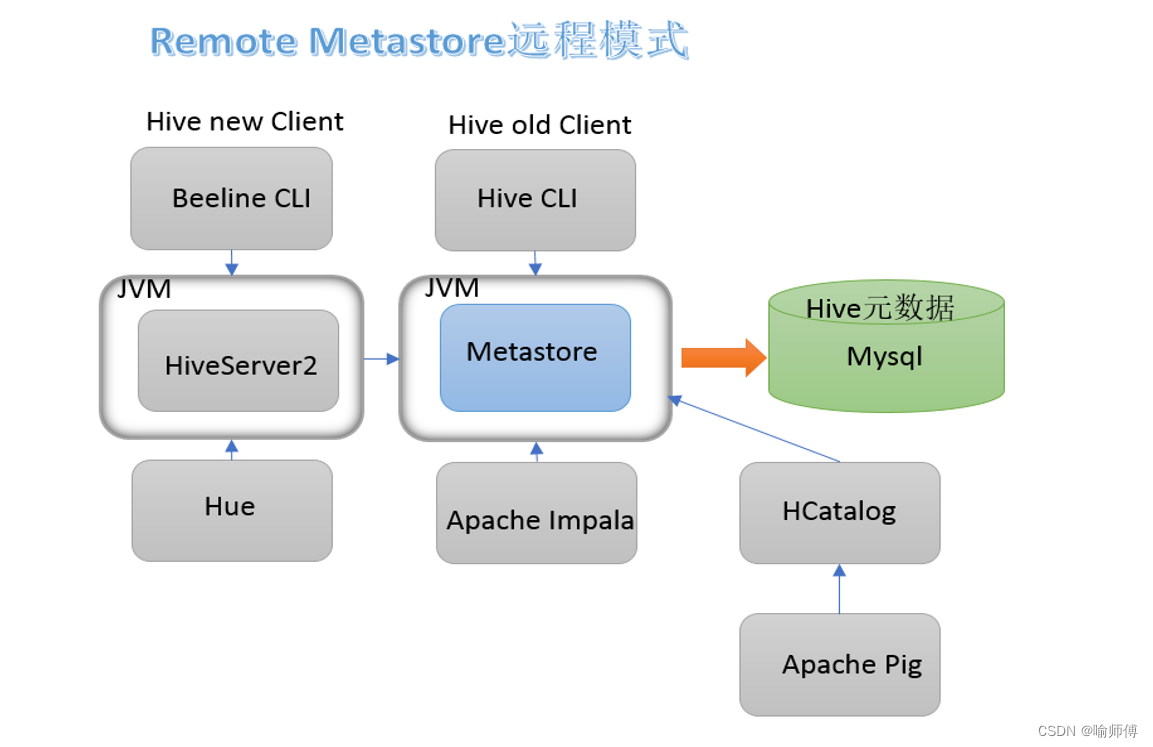
- Beeline 是一个全新的 Hive 客户端工具,它使用 JDBC 连接到 HiveServer2,并提供了更加现代化和稳定的命令行界面。与 Hive CLI 不同,Beeline 使用
Apache Hive Thrift JDBC驱动程序连接到 HiveServer2。 - 优点:Beeline 具有性能更好、稳定性更高的优点,同时支持更多的特性和功能,如 Kerberos 认证、SSL 加密等。
- 缺点:相比于 Hive CLI,Beeline 的学习曲线可能稍微陡峭一些,而且在一些早期版本中可能存在一些 Bug。

- Beeline 是一个全新的 Hive 客户端工具,它使用 JDBC 连接到 HiveServer2,并提供了更加现代化和稳定的命令行界面。与 Hive CLI 不同,Beeline 使用
尽管 Hive CLI 在一些场景下仍然可以使用,但建议尽可能使用 Beeline,特别是对于新的 Hive 部署和项目。Beeline 提供了更好的性能、稳定性和功能支持,能够更好地满足现代数据处理的需求。