自动驾驶融合定位：kalman 滤波器基本原理

一、概述

kalman滤波是一个重要的融合手段，虽然最近几年，随着基于优化的方法不断推广，基于滤波的方法逐渐式微，但是，由于二者各有优缺点，滤波方法现在及将来都仍然是重要的融合手段之一。

在多传感器融合定位系统中，kalman解决的其实是这样一个任务

它的本质是，结合预测与观测，得到最“精确”的后验值。实际中，预测与观测均从传感器而来（预测往往从IMU、编码器等传感器递推而来，观测往往从GPS、雷达、相机等传感器而来），因此滤波器的作用便是结合各传感器得到一个最好的融合结果。

kalman滤波的推导会显得很复杂，而且有多种推导方式，我们理解其中一种就可以，大可不必全都掌握。就像孔乙己会沾沾自喜地告诉别人，茴香的茴有四种写法，没多大用处（当然，这里指的是工作人员，如果是研究滤波理论的，那深入到多深都不为过，就像如果你是专门研究汉字的，茴香的茴了解这四种写法可能都不够，还要研究它的演化史，甚至不同地域的不同发音）。

关于工程人员的理论深度，我们可以在本篇文章末尾再更详细地讨论一次。

附赠自动驾驶学习资料和量产经验：链接

二、概率基础知识

kalman 滤波的推导会用到大量的概率基础知识，为了后面的推导过程更流畅，我们就先把基础知识解决了。

1.概率、概率密度

上图中， 𝑝(𝑥) 为x在区间[a,b]上的概率密度，它表示的是随机变量在区间的分布情况。 𝑃𝑟 代表的是x在区间[c,d]上的概率，它是概率密度的积分

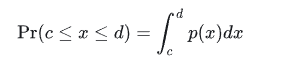
我们平时所说“高斯分布”、“非高斯分布”均是指它的概率密度。

2.联合概率密度

𝑥∈[𝑎,𝑏] 和 𝑦∈[𝑟,𝑠] 的联合概率密度函数可以表示为 𝑝(𝑥,𝑦) ，其积分表示x和y同时处在某个区间的概率，满足下式

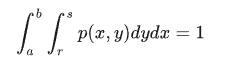
特别地，当x和y统计独立的时候，有

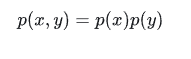
3.条件概率密度

4.贝叶斯公式

5.贝叶斯推断

6. 高斯概率密度函数

7. 联合高斯概率密度函数

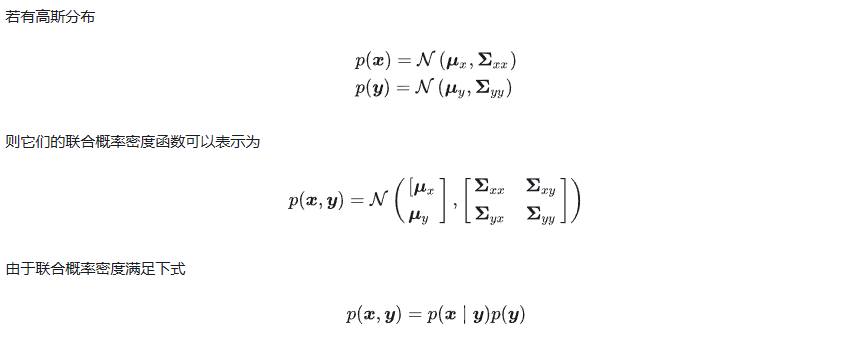
该式在高斯分布的前提下可以重新分解。

8. 高斯随机变量的线性分布

在上面的例子中，若已知x和y之间有如下关系

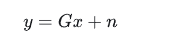
同理可得：

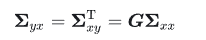
三、滤波器推导

由于kalman滤波是贝叶斯滤波的一种（如下图），而贝叶斯滤波又是递推式状态估计的一种，我们得从大到小把这些东西讲一讲，逐渐缩小到kalman滤波这个地方，这样容易把问题讲清楚。

1.状态估计模型

实际状态估计任务中，待估计的后验概率密度可以表示为

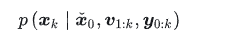
图模型中体现了马尔可夫性，即当前状态只跟前一时刻状态相关，和其他历史时刻状态无关。

该性质的数学表达为：

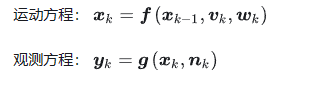
2. 贝叶斯滤波

这种公式表达形式，其实就可以称为是贝叶斯滤波了。根据以上结果，可以画出贝叶斯滤波的信息流图如下

3.kalman滤波推导

终于进入到了这个环节，不过要说明的是，我们这里kalman滤波的推导并不是按照上面贝叶斯滤波的表达形式去推的，上面贝叶斯滤波的讲述只是为了从更大的角度说明kalman是贝叶斯滤波的一种，这样更容易理解它的本质。此处推导kalman的方式是广义高斯滤波。

上面三个方程与之前所述预测方程(如下)，就构成了卡尔曼经典五个方程

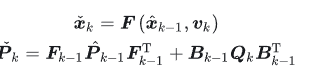
需要说明的是，若不把第二节8中的结果带入，而保留原始形式，则对应的五个方程被称为广义高斯滤波。

4.扩展kalman滤波(EKF)推导

当运动方程或观测方程为非线性的时候，无法再利用之前所述的线性变化关系进行推导，常用的解决方法是进行线性化，把非线性方程一阶泰勒展开成线性。即

根据该线性化展开结果，可以得到预测状态的统计学特征为

把均值和方差的具体形式，带入广义高斯滤波的公式，最终得到EKF下得经典五个公式

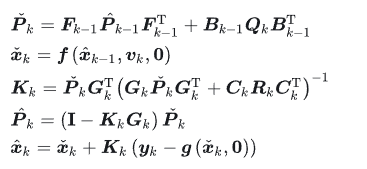
5. 迭代扩展卡尔曼滤波(IEKF)推导

由于非线性模型中做了线性化近似，当非线性程度越强时，误差就会较大。但是，由于线性化的工作点离真值越近，线性化的误差就越小，因此解决该问题的一个方法是，通过迭代逐渐找到准确的线性化点，从而提高精度。

四、kalman滤波的物理理解

我个人有个习惯，就是喜欢从物理意义上去理解公式，而且我也坚持认为，只有从物理意义上理解了，才算是真正的理解了（虽然我还没有完全做到这一点，很多公式我还没有在物理上给出让自己信服的解释）。

公式是用来实现算法的，而不是理解算法的，这二者之间有非常大的区别。物理史上，很多好的理论创建的时候，也都是从一个简单的物理假设出发，再去用公式去证明它的正确性和梳理它的实现过程。

我们先再次列出kalman的这五个公式

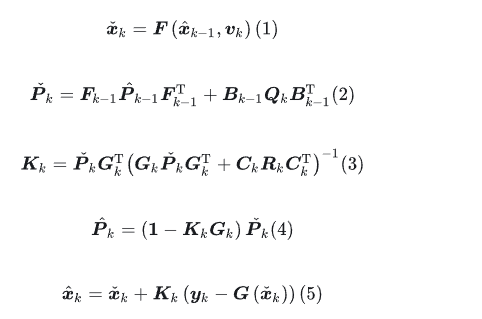
为了更好地理解它的物理意义，我们把(5)式拆开，并把这些公式重新排一下顺序(注意这个顺序并不是实际计算的顺序，只是方便理解)，在每个公式前面加上它的物理意义。

这一步需要解释一下了：

那么啰嗦了这么一大堆，其实我们可以看到，kalman的物理意义其实就是“把预测的值和观测的值做一个加权，而且这个加权权重是用方差计算的”。现在再回过头去看概述中的那张图，应该可以更好地理解了吧。

五、总结

kalman 推导的内容倒没什么可总结的了，此处可以讨论一下开头提到的那个话题，即工程人员到底应该对理论的掌握深入到什么程度。当然，这是一个开放性的话题，没有标准答案，我也只是表达我个人观点而已，抛砖引玉，不一定对。

首先理论是为工程服务的（仅限于工程领域），这个应该没什么疑问，那么理论的掌握就本着“够用”就好，怎样理解“够用”，我认为它包括两点，第一，是要理解它的物理含义，第二，是要能够在它因任务的不同而发生变化时，能相应地做出理论上的修改。对于这里的 kalman 来讲，它的物理含义我们已经介绍过了，完全可以用这五个公式描述，而变化，实际工程中，倒并没有需要kalman做过多的变化（那些停留在论文里，但很少被工程化的那些改进版的kalman滤波理论以外）。这样看，单单对于kalman来讲，我认为，即使一种推导方式都不会，也没啥大不了的，仍然可以理直气壮，不用觉得低人一头。真正应该感到羞愧的，是那些公式推导很熟悉，但是对这些方法在实际系统中表现出的优缺点却知之甚少的人。

必须说明的是，前面仅仅是对kalman这一件事来讲，它的五个公式已经满足“够用”的标准，对于其他事，比如前面讲的误差模型推导，那就真的得掌握了，因为不同传感器、甚至同一传感器不同精度，所需要的误差模型都不一样，这种灵活多变的需求，使它的结论本身不能满足“够用”的标准。

这个观点可能很多人并不同意，应该用的最多的反对理由就是“理论深度不够怎么行，况且理论掌握的深了又没有什么坏处”。对于前半句，其实我们通过对“够用”的分析，算是已经反驳过了，对于后半句，倒也不能说错，毕竟技多不压身嘛，不过我们应该注意到的是，这个“多”是要付出代价的，最宝贵的代价当属时间，在校生要挤更多时间做课题，工作的能抽出时间学习已经不容易，即使有一些时间，还想着去搞搞自己的kpi，总之，应该没有谁的时间是无限的。那么，这时候，刚才的后半句就得变成“在付出代价的情况下，相比于理论掌握的深入，他俩谁的价值更大”，相信大家肯定明白我在说什么。

一刀切（越多越好）谁都会，权衡（资源有限情况下的取舍）才是最难的事情，它需要认清每件事情的价值，这需要不间断的思考，甚至称得上是一门艺术。