目录
1.集合
2.集合的相关操作
(1)查(Find):
•Find操作的优化
(2)并(Union):
•Union操作的优化
1.集合
数据元素之间的逻辑关系可以为集合,树形关系,线性关系,图关系。对于集合而言,一个集合可以划分为若干个互不相交的子集。在集合下,两个元素之间的关系只有两种,即从属于同一个子集或从属于不同子集。
那么怎么表示这样的关系呢?在讲解森林时,提到过森林的概念,即互不相交的树的集合,那么在这里,我们可以把不同子集的元素放到不同的树中表示。
2.集合的相关操作
并查集(Disjoint Set)是逻辑结构,也就是对集合的一种具体实现,只进行“并”和“查”两种基本操作。
(1)查(Find):
•要想找到某一个元素属于哪一个集合,可以从指定元素出发,一路向上找到其唯一对应的根节点(有几个根节点,就有几棵树,就有几个集合)。
在树的存储结构中,我们讲了双亲表示法,孩子表示法,孩子兄弟表示法,用哪种方法表示集合比较合适呢?
因为在集合中,需要向上找到根节点,显然使用双亲表示法更加方便。即,用一个静态数组,就能表示出父子的关系。忘记了可以看看:树
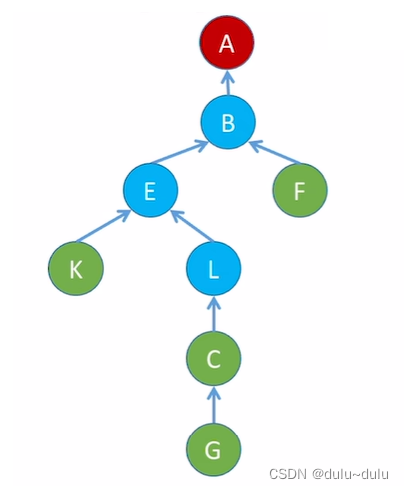
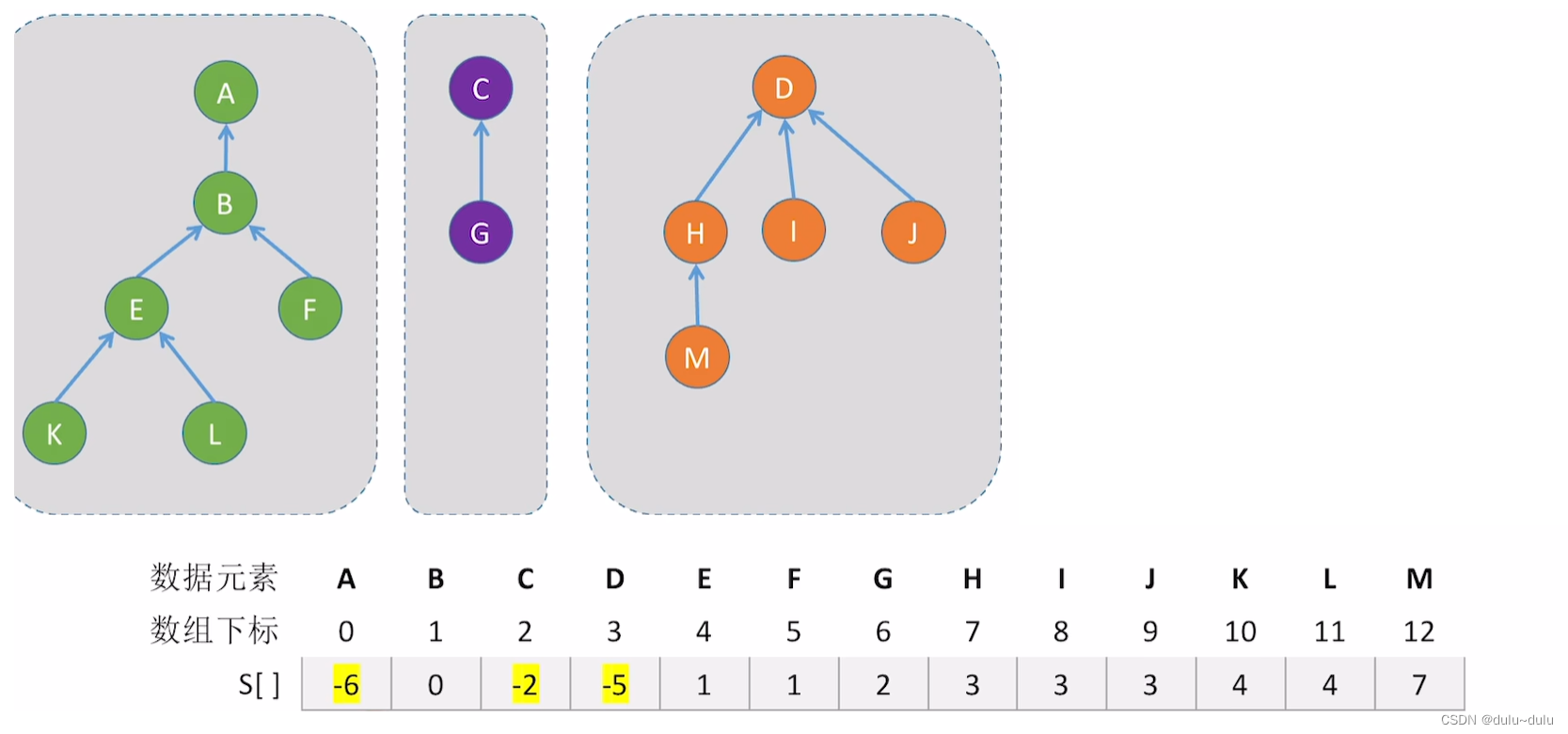
例如下图,元素L的数组下标是11,其父节点为数组下标为4的元素,即E,如此推上去,直到推到数组下标为0的元素,就是根节点了。
① 初始化并查集,将各个元素初始化为各自独立的子集。
#define SIZE 13
int UFSets[SIZE]; //集合元素数组//初始化并查集
void Initial(int s[]){for(int i=0;i<SIZE;i++)s[i]=-1;
}
② 查操作
// Find 操作,找 x 所属集合(返回 x 所属根结点)
int Find(int s[], int x) {while (s[x] >= 0)x = s[x]; // 循环寻找 x 的根return x; // 返回根节点的下标
} 时间复杂度:
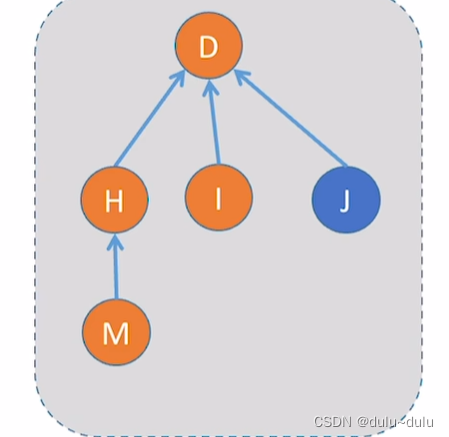
对于下图,如果想查找J元素所属的集合,只需要向上找一次就可以找到根节点。
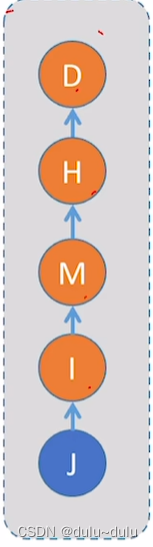
但是对于下图,就需要向上找很多层,才能找到根节点。
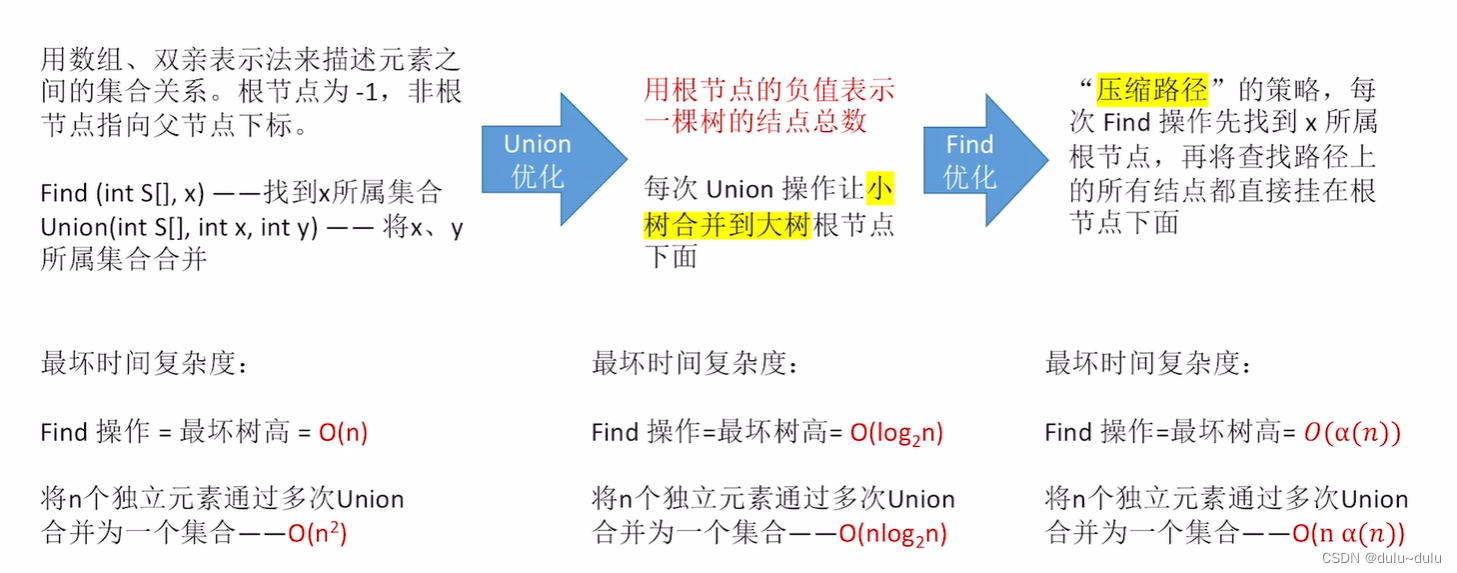
所以,若节点数为n,Find最坏时间复杂度为O(n),可以看到Find最坏时间复杂度与高度h直接相关,所以优化并查集的效率时,可以在合并树时减小树的高度。这一点留到“合并树”的时候讲。
•如果想判断两个元素是否属于同一个集合,那就分别查找两个元素的根节点,判断根节点是否相同。
bool Compare(int Root1, int Root2) {if (Find(Root1) == Find(Root2))return true;elsereturn false;
}•Find操作的优化
之前使用的Find操作是从指定节点出发,根据s[ ],向上找到所属根节点,这样向上的路径称为“查找路径”,而Find的优化操作就是要压缩这条路径,即“压缩路径”。具体操作就是先找到根节点,再将查找路径上所有结点都挂到根结点下。
例如下图,是执行节点L的查找路径:
压缩路径就是将图中蓝色的节点全部挂到A节点下。这样,从L节点向上找根节点的路径就被压缩了。
优化代码如下:
//Find"查"操作优化,先找到根节点再进行"压缩路径"
int Find(int S[],int x){int root = x;while(S[root]>=0) root=S[root]; //循环找到根while(x!=root){ //压缩路径int t=S[x]; //t指向x的父节点S[x]=root; //x直接挂到根节点下 x=t;}return root; //返回根节点编号
}每次 Find 操作,先找根,再“压缩路径”,可使树的高度不超过O((n))。
(n)是一个增长很缓慢的函数,对于常见的n值,通常
(n)≤4,因此优化后并查集的Find、Union操作时间开销都很低。
具体地,Find最坏时间复杂度为,将n个独立元素通过多次Union合并为一个集合的最坏时间复杂度为
(n个元素需要合并n-1次)。
(2)并(Union):
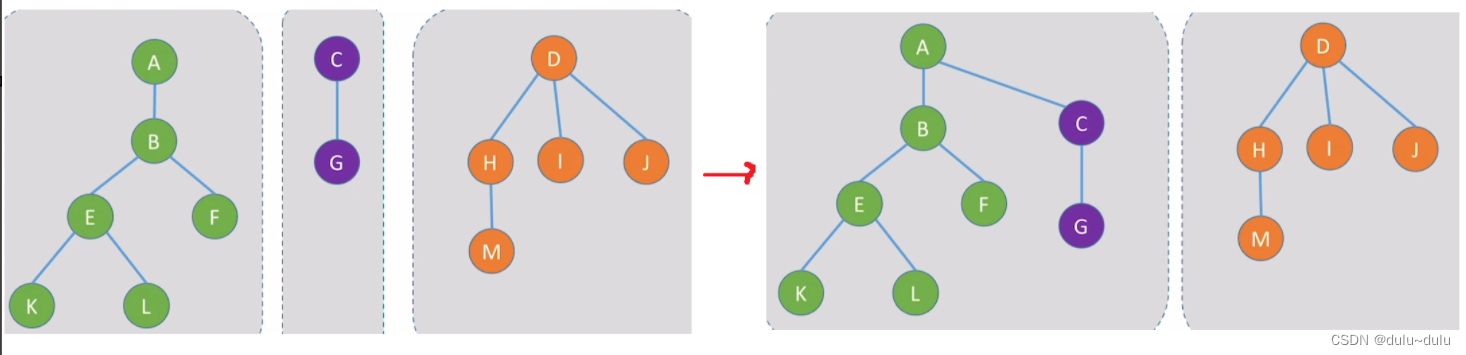
•要想将两个集合“并”为同一个集合,可以将一棵树作为另外一棵树的子树。
//Union"并"操作,将两个集合合并为一个
void Union(int s[],int Root1,int Root2){//要求Root1与Root2是不同的集合if(Rootl==Root2) return;//将根Root2连接到另一根Root1下面S[Root2]=Root1;
}
//时间复杂度:O(1)S[Root2]=Root1达到的效果如下(假设要将以C为根节点的树合并为以A为根节点的子树):
刚开始Root1 = 0;Root2 = 2;将S[2]=0
也就是将C的父节点指向0号元素A
若想将n个独立元素通过多次Union合并为一个集合,最坏时间复杂度为O(n^2)。因为要合并n个独立的元素,需要n-1次Union,每一次Union之前需要从指定节点出发找到两个集合的根节点,而Find操作时间复杂度为O(n),所以重复n-1次的Union,最坏时间复杂度为O(n^2)。
•Union操作的优化
为了使“查”的效率更高,合并树时可以让小树合并到大树中,这样就不会增加树的高度了。
那么如何表示一棵树的大小呢?可以用根节点的绝对值表示树的结点总数。
例如下图2,以A为最左边树的根节点,A所对应的数组的值为-6,|-6|就是这棵树的节点总数。同理,以C为根节点的树有两个节点,以D为根节点的树有5个节点。
优化代码如下:
//Union"并"操作,小树合并到大树
void Union(int S[],int Rootl,int Root2){if(Rootl == Root2) return;if(S[Root2]>S[Root1]){ //Root2结点数更少 S[Root1]+= S[Root2]; //累加结点总数S[Root2]=Rootl; //小树合并到大树} else {S[Root2]+= S[Root1]; //累加结点总数S[Root1]=Root2; //小树合并到大树}
}
//改进的Union操作时间复杂度依旧是O(1)用该方法优化“Union”操作后,构造的树高不超过,那么Find操作的最坏时间复杂度也能到O(
),将n个独立元素通过多次Union合并为一个集合的最坏时间复杂度为O(n*log2^n)
总结: