此篇文章与大家分享递归、搜索与回溯算法关于穷举vs暴搜vs深搜的专题
如果有不足的或者错误的请您指出!
目录
- 1.全排列
- 1.1解析
- 1.2题解
- 2.子集
- 2.1解析
- 2.1.1解法1
- 2.1.2解法1代码
- 2.1.3解法2
- 2.1.4解法2代码
1.全排列
题目:全排列
1.1解析
假设nums = [1,2,3]
对于这种列举的题,我们的第一步通常是画决策树
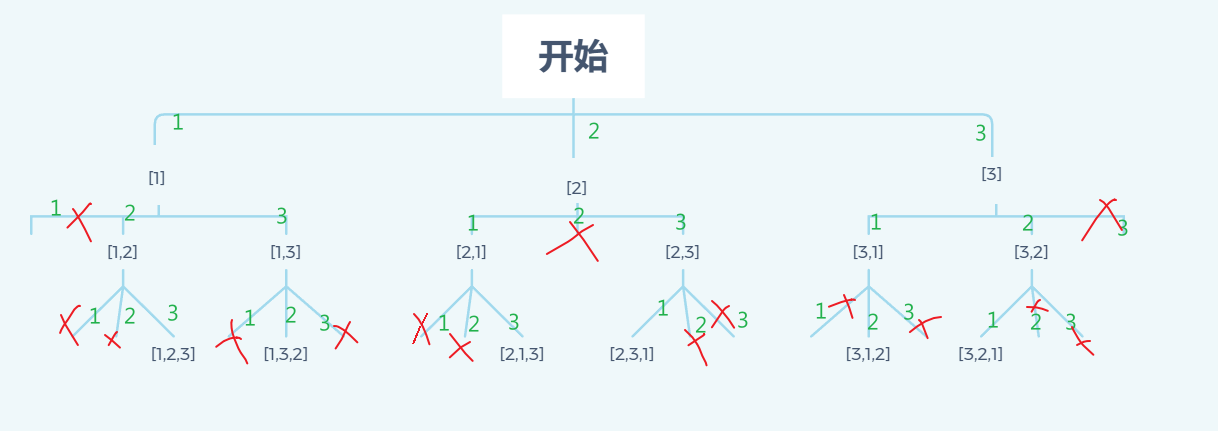
如图所示,我们按照要求将决策树显示画出来后,可以发现,实际上就是我们前面讲过的二叉树的遍历
只不过之前的题目已经帮我们把树给画好了,但是这类题目需要我们自己画
按照图,我们发现,实际上对于每一个节点,我们做的事情都是一样的,都是针对三种情况进行讨论,那么我们就可以使用递归来做
此时有几个主要的细节问题
(1)剪枝:如图所示,我们有一些枝干是不用去递归的(图中的红叉叉),就是我们已经讨论过的数字就不能再次讨论的.
我们可以创建一个布尔类型数组,长度与nums数组一样,用于表示当前下标在nums中的值是否已经讨论过
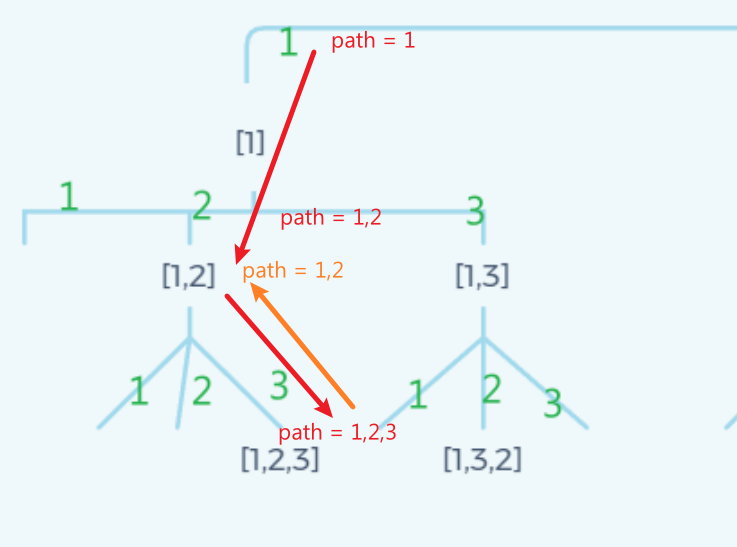
(2)记录:我们用path来记录遍历每一条枝干的节点的值,当path里面值的长度 = nums数组的长度是,我们就将path插入到返回列表中
(3)回溯:我们在递归完某个枝干后,需要将path还原成原来的样子
1.2题解
java">class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;public List<List<Integer>> permute(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];dfs(nums);return ret;}private void dfs(int[] nums) {if(path.size() == nums.length) {ret.add(new ArrayList(path));return;}for(int i = 0; i < nums.length; i++){if(check[i] == false) {path.add(nums[i]);check[i] = true;dfs(nums);//回溯check[i] = false;path.remove(path.size()-1);}}}
}
2.子集
题目:子集
2.1解析
2.1.1解法1
假设数组nums = [1,2,3]
我们直接画决策树

此时我们可以发现,决策树的叶子节点就是我们想要的结果,此时叶子节点也就是递归的出口
而每一个节点做的事情都是一样的,就是选与不选进行分枝
但是此处我们的递归函数还要传一个参数,就是告诉下一次递归选的数是哪个
2.1.2解法1代码
java">class Solution {private List<List<Integer>> ret = new ArrayList<>();private List<Integer> path = new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {dfs(nums,0);return ret;}private void dfs(int[] nums,int pos) {if(pos == nums.length){ret.add(new ArrayList(path));return;}path.add(nums[pos]);dfs(nums,pos+1);path.remove(path.size()-1);dfs(nums,pos+1);}
}
2.1.3解法2
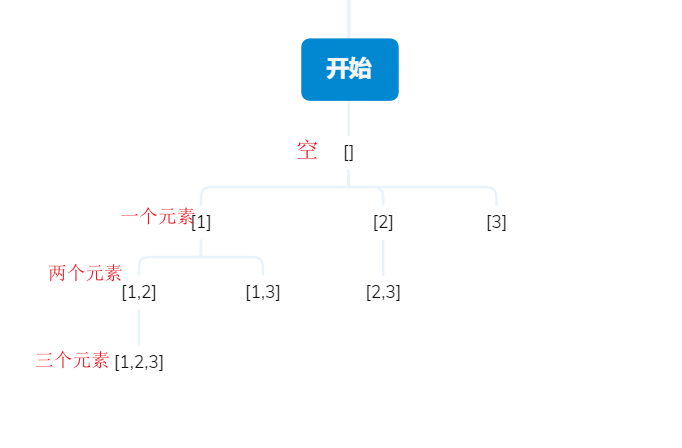 如图所示的决策图,我们可以以path中元素的个数为标准进行递归,每次递归都从当前传进去的pos开始添加元素,就能保证不重复
如图所示的决策图,我们可以以path中元素的个数为标准进行递归,每次递归都从当前传进去的pos开始添加元素,就能保证不重复
此时我们会发现,每一个节点都是我们要的结果,这种解法相对于解法1来说"剪枝"了很多情况
2.1.4解法2代码
java">class Solution {private List<List<Integer>> ret = new ArrayList<>();private List<Integer> path = new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {dfs(nums,0);return ret;}private void dfs(int[] nums,int pos) {ret.add(new ArrayList<>(path));for(int i = pos; i < nums.length; i++){path.add(nums[i]);dfs(nums,i+1);path.remove(path.size()-1);}}
}