思路

1. dp数组定义：到下标为i， j 的地方共有dp[i][j]条路径
2. 递推公式：在当前节点不是障碍物时，dp[i][j] = dp[i][j-1] + dp[i-1][j]，否则就是为0
3. dp数组初始化：dp[0][0]初始化也需要做判断
4. 遍历顺序：自左向右，自上而下
5. 时间复杂度：     

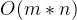
代码

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size(), n = obstacleGrid[0].size();vector< vector<int>> dp(m, vector<int>(n));if(obstacleGrid[0][0] == 0) dp[0][0] = 1;for(int j = 1; j < n; j++){if(obstacleGrid[0][j] == 0){dp[0][j] = dp[0][j-1];}}for(int i = 1; i < m; i++ ){if(obstacleGrid[i][0] == 0){dp[i][0] = dp[i-1][0];}}  for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){if(obstacleGrid[i][j] == 0){dp[i][j] = dp[i][j-1] + dp[i-1][j];}}}return dp[m-1][n-1];}
};