【八大排序（一）】插入排序与希尔排序

❣博主主页: 33的博客❣
▶️文章专栏分类:八大排序◀️
🚚我的代码仓库: 33的代码仓库🚚
🫵🫵🫵关注我带你了解更多排序知识

在这里插入图片描述

1.前言

所谓排序，就是把一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。在日常生活中，排序的应用十分广泛，比如大家最讨厌的就是读书时期的按照名次排序，还有在打牌时，也会用到排序，那么就搞快来和博主一起学习吧！！！

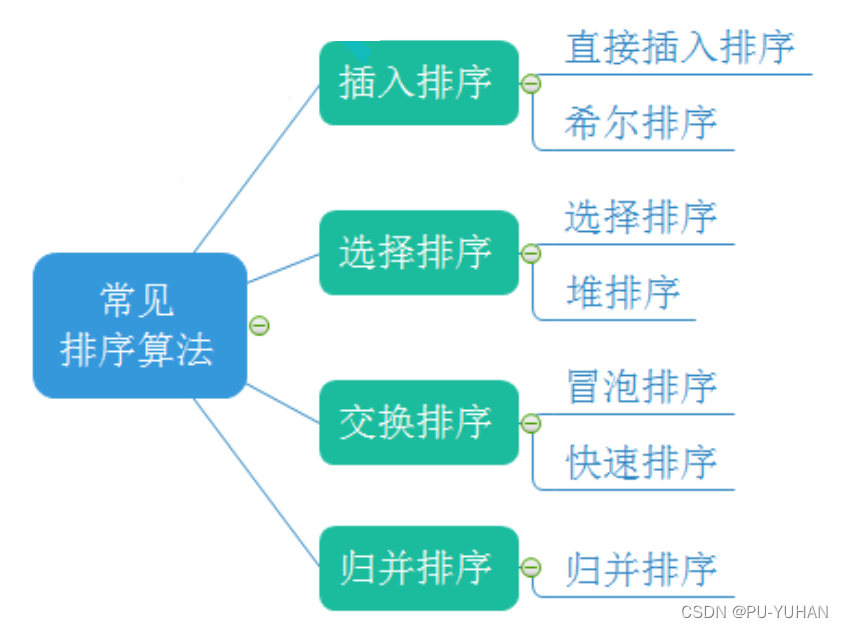
2.常见算法>排序算法

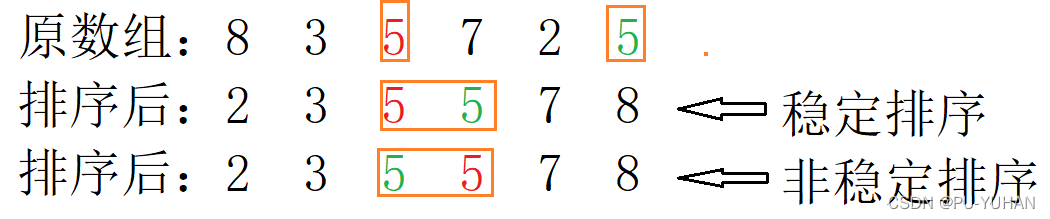
在这里插入图片描述

3.稳定性

稳定性就是，当一个算法>排序算法对一个数组排序的时候，两个相同的数，在排序后相对位置有没有发生变化。如下：
在这里插入图片描述

4.插入排序

在实际生活中，玩扑克牌就用到了插入排序
在这里插入图片描述

4.1概念

把待排序序列按其关键值得大小插入到一个已经排好序的序列中，直到所有记录插入为止。

4.2直接插入排序

画图理解：
当已经有一组有序的序列时【1，2，4，5】，插入就一个元素【3】

插入排序

代码实现：

public int[] insertOrder(int[] arr){for (int i=1;i<arr.length;i++){int tmp=arr[i];int j=i-1;for (;j>=0;j--){if(arr[j]>tmp){arr[j+1]=arr[j];}else break;}
//            while (j>=0&&arr[j]>tmp){
//                arr[j+1]=arr[j];
//                j--;
//            }arr[j+1]=tmp;}return arr;}

时间复杂度:O( $n^2$ )
空间复杂度：O(1)
稳定性：稳定

4.3希尔排序

希尔派苏又称缩小增量法。希尔排序的基本思想：先选定一个整数，把待排序文件中所有记录分成多个组，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达gap=1时，所有记录在统一组内排好序
分组排序：
分组的时候可以挨着分，也可以岔着分，那么具体该用那种分组方式呢？
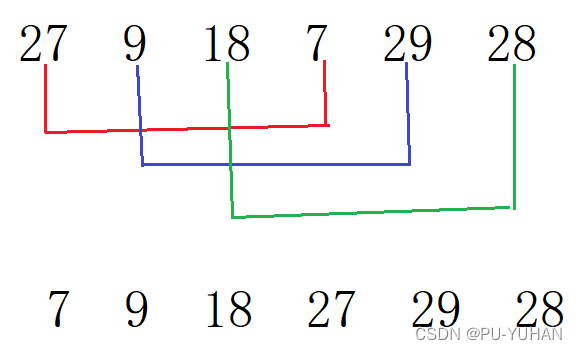
在这里插入图片描述

观察上诉两种分组方式，我们发现岔开分会让数组更有序，小数据在左边，大数据在右边，更利于插入操作。

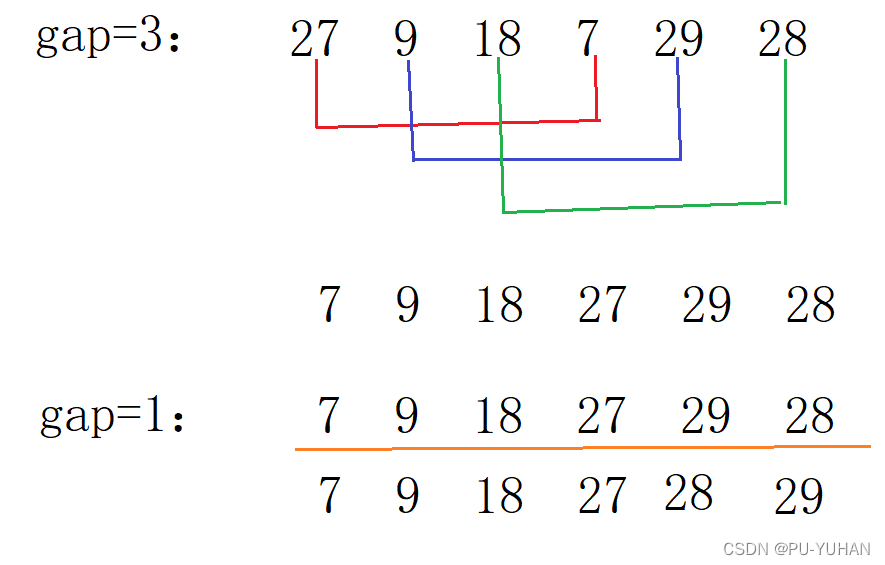
希尔排序总结：

希尔排序是对直接插入排序的优化。
当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定。我们暂时就按照O（ $n^{1.25}$ ）到O（ $1.6*n^{1.25}$ ）来算。

代码实现：

public int[] shellOrder(int[] arr){int gap=arr.length;while (gap>1){gap=gap/2;shell(arr,gap);}return arr;}private void shell(int[] arr, int gap) {for (int i=gap;i<arr.length;i++){int tmp=arr[i];int j=i-gap;for (;j>=0;j-=gap){if(arr[j]>tmp){arr[j+gap]=arr[j];}else break;}arr[j+gap]=tmp;}}

时间复杂度O（ $n^{1.25}$ ）到O（ $1.6*n^{1.25}$ ）
空间复杂度：O(1)
稳定性：不稳定

5.总结

本篇文章主要介绍了八大排序中的其中两个排序：直接插入排序和希尔排序，以及它们的时间复杂度，空间复杂度，稳定性都是需要我们好好掌握的，下篇文章博主将继续和大家分享选择排序。
最后大家分享一个网站：https://visualgo.net/en
这是一个在学习八大排序时，便于我们理解的一个网站，里面有许多算法>排序算法，可以通过图形结合，帮助我们更好的学习。
在左上角可以切换中英文：