【数据结构】插入排序

1.简单插入排序

1.1 基本思想

假设待排序记录集合为 $R_{1}$ ， $R_{2}$ ，... ， $R_{n}$ 简记为 $[1...n]$ 。插入排序方法由 $n$ 趟组成，假设要进行第 $i$ 趟，此时第 $1$ ~ $i-1$ 个记录已经插入排好序，第 $i$ 趟是将第 $i$ 个记录插入到有序序列中，使之仍然有序。

1.2 算法实现

//直接插入排序
void InsertSort(int A[], int n) {int i, j, temp;for(i = 1; i < n; i++) {        //将各元素插入已排好序的序列中if(A[i] < A[i - 1]) {       //若A[i]关键字小于前驱temp = A[i];            //用temp暂存A[i]for(j = i - 1; j >= 0 && A[j] > temp; j--)   //检查所有前面已排好序的元素A[j + 1] = A[j];    //所有大于temp的元素都向后挪位A[j + 1] = temp;        //复制到插入位置}}
}

定义一个变量 $i$ 指向当前需要处理的元素，并用中间变量 $temp$ 将 $i$ 保存起来（防止移动元素时覆盖掉原有元素）

依次检查前面已经排好序的元素，如果大于 $temp$ ，则向后挪位，当 $j$ = $-1$ 时遍历完成，将 $temp$ 的值复制到插入位置。

1.3 算法效率分析

空间复杂度： $O(1)$

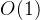
时间复杂度：主要来自对比关键字、移动元素，若有 $n$ 个元素，则需要 $n-1$ 趟排序

最好情况：共 $n-1$ 趟处理，每一趟只需要对比关键字1次，不用移动元素

最好时间复杂度—— $O(n)$

最坏情况：原本为逆序排序

最坏时间复杂度—— $O(n^2)$

平均时间复杂度： $O(n^2)$

算法稳定性：稳定

2. 优化——折半插入排序

2.1 思路

先用折半查找找到应该插入的位置，再移动元素

当 low > high 时折半查找停止，应将 [low, i - 1] 内的元素全部右移，并将A[0] 复制到 low 所指位置

当A[mid] == A[0] 时，为了了保证算法的“稳定性”，应继续在 mid 所指位置右边寻找插入位置

2.2 算法实现

//折半插入排序
void InsertSort(int A[], int n) {int i, j, low, high, mid; for(i = 2; i <= n; i++) {          //依次将A[2]~A[n]插入到前面已排序的序列A[0] = A[i];                   //将A[i]暂存到A[0]low = 1;                       //设置折半查找的范围high = i - 1;while(low <= high) {           //折半查找，确定插入位置mid = (low + high) / 2;    //折半if(A[mid] > A[0]) {        //插入点在低半区high = mid - 1;} else {                   //插入点在高半区low = mid + 1;}}for(j = i - 1; j >= high + 1; j--) {A[j + 1] = A[j];           //统一后移元素，空出插入位置}A[high + 1] = A[0];            //插入操作}
}

3.希尔排序（Shell Sort）

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。

3.1 基本思想

根据插入排序的特点，当元素比较少时效率比较高；或者，当元素已经基本有序时，效率比较高。开始时，把元素分为几组，组内元素是比较少的，因此组内插入排序效率比较高，每进行一趟后，增加组内元素的个数，与此同时，元素也越来越有序，效率也会越来越高。

先将待排序表分割成若干形如 $L[i,i+d,i+2d,... ,i+kd]$ 的“特殊”子表，对各个子表分别进行直接插入排序。缩小增量d，重复上述过程，直到 d=1 为止

先追求表中元素部分有序，再逐渐逼近全局有序

3.2 算法实现

//希尔排序
void ShellSort(int A[], int n) {int d, i, j;//A[0]只是暂存单元，不是哨兵，当j<=0时，插入位置已经找到for(d = n/2; d > 0; d /= 2) {        //步长变化for(i = d + 1; i <= n; i++) {    //插入排序if(A[i] < A[i-d]) {          //需将A[i]插入有序增量子表A[0] = A[i];             //暂存在A[0]for(j = i-d; j > 0 && A[0] < A[j]; j -= d) {A[j+d] = A[j];       //记录后移，查找插入位置}A[j+d] = A[0];           //插入}}}
}

3.3 算法性能分析

空间复杂度： $O(1)$

时间复杂度：和增量序列 $d_{1}$ , $d_{2}$ , $d_{3}$ ... 的选择有关，目前无法用数学手段证明确切的时间复杂度，最坏时间复杂度为 $O(n^2)$ ，当n在某个范围内时，可达 $O(n^{1.3})$

稳定性：不稳定！

适用性：仅适用于顺序表，不适用于链表