【LetMeFly】3244.新增道路查询后的最短距离 II：贪心（跃迁合并）-9行py（O(n)）

力扣题目链接：https://leetcode.cn/problems/shortest-distance-after-road-addition-queries-ii/

给你一个整数 n 和一个二维整数数组 queries。

有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（ 0 <= i < n - 1）。

queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。

所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的长度。

 

示例 1：

输出： [3, 2, 1]

解释：

新增一条从 2 到 4 的道路后，从 0 到 4 的最短路径长度为 3。

leetcode.com%2Fuploads%2F2024%2F06%2F28%2Fimage9.jpg&pos_id=img-N5uGm0Hx-1732080025470%29" />

新增一条从 0 到 2 的道路后，从 0 到 4 的最短路径长度为 2。

leetcode.com%2Fuploads%2F2024%2F06%2F28%2Fimage10.jpg&pos_id=img-fH2gffWA-1732080027237%29" />

新增一条从 0 到 4 的道路后，从 0 到 4 的最短路径长度为 1。

示例 2：

输出： [1, 1]

解释：

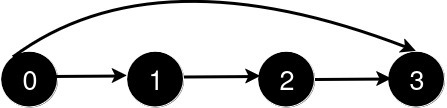
新增一条从 0 到 3 的道路后，从 0 到 3 的最短路径长度为 1。

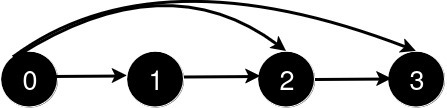
新增一条从 0 到 2 的道路后，从 0 到 3 的最短路径长度仍为 1。

 

提示:

• 3 <= n <= 105
• 1 <= queries.length <= 105
• queries[i].length == 2
• 0 <= queries[i][0] < queries[i][1] < n
• 1 < queries[i][1] - queries[i][0]
• 查询中不存在重复的道路。
• 不存在两个查询都满足 i != j 且 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

解题方法：跃迁合并

把每一条路径视为一条跃迁通道，每个点记录“自己最多能跃迁到的点”，初始值每个点能跃迁到的点都是自己的下一个节点。

新来一条“跃迁通道”有两种可能：

• 被一条更长(或等长)的跃迁通道覆盖
• 覆盖n条跃迁通道

反正不可能和其他跃迁通道有交叉。

两种情况的判断方式是“跃迁起点”指向的“能跃迁到的点”是否大于(等于)自己的“跃迁终点”

例如新加一条[1, 3]的跃迁路径，结果发现1已经能跃迁到5了，那么就说明这是一条被其他“跃迁通道”覆盖的通道

• 对于第一种情况：直接continue

• 对于第二种情况：修改所有“最大被覆盖子跃迁通道”的起点的“能跃迁到的点”

  例如原本有“跃迁通道”[1, 3]，[3, 4]，[4, 7]，新增“跃迁通道”[1, 7]，

  那么就将1、3、4的“能跃迁到的点”修改为7。

  跃迁次数减少$3-1=2$次

时空复杂度分析

• 时间复杂度$O(n+q)$：每次修改一个点“能跃迁到的点”，总跃迁次数就会减少一；总跃迁次数最多减少到1，说明“跃迁合并”最多$n-1$次。
• 空间复杂度$O(n)$，返回值不计入。

AC代码

C++

/*
每个点记录“自己跃迁到的点”
初始值每个点能跃迁到的点都是自己的下一个节点新来一条“跃迁通道”有两种可能：+ 被一条更长(或等长)的跃迁通道覆盖+ 覆盖n条跃迁通道
反正不可能和其他跃迁通道有交叉
两种情况的判断方式是“跃迁起点”指向的“能跃迁到的点”是否大于(等于)自己的“跃迁终点”+ 对于第一种情况：直接continue+ 对于第二种情况：修改所有“最大被覆盖子跃迁通道”的起点的“能跃迁到的点”
*/
// FourthTry  // 简化版  // 执行用时分布:2ms,击败98.51%;消耗内存分布:108.84MB,击败83.86%.
class Solution {
public:vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {vector<int> transitionTo(n), ans(queries.size());for (int i = 0; i < n; i++) {transitionTo[i] = i + 1;}int transitionToEndTimes = n - 1;for (int i = 0; i < queries.size(); i++) {int from = queries[i][0], to = queries[i][1], now = from;while (transitionTo[now] < to) {transitionToEndTimes--;int originalTo = transitionTo[now];transitionTo[now] = to;now = originalTo;}ans[i] = transitionToEndTimes;}return ans;}
};

Python

from typing import Listclass Solution:def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:transitionTo = [i + 1 for i in range(n)]ans = []shortestTimes = n - 1for from_, to in queries:while transitionTo[from_] < to:shortestTimes -= 1transitionTo[from_], from_ = to, transitionTo[from_]ans.append(shortestTimes)return ans

Java

class Solution {public int[] shortestDistanceAfterQueries(int n, int[][] queries) {int[] transitionTo = new int[n];for (int i = 0; i < n; i++) {transitionTo[i] = i + 1;}int[] ans = new int[queries.length];int minTimes = n - 1;for (int i = 0; i < queries.length; i++) {int from = queries[i][0], to =  queries[i][1];while (transitionTo[from] < to) {minTimes--;int originalTo = transitionTo[from];transitionTo[from] = to;from = originalTo;}ans[i] = minTimes;}return ans;}
}  // AC,100.00%,79.09%

Go

package mainfunc shortestDistanceAfterQueries(n int, queries [][]int) (ans []int) {transitionTo := make([]int, n)for i := range transitionTo {transitionTo[i] = i + 1}minTimes := n - 1for _, query := range queries {from, to := query[0], query[1]for transitionTo[from] < to {minTimes--transitionTo[from], from = to, transitionTo[from]}ans = append(ans, minTimes)}return
}  // AC,81.82%,29.41%

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/143908539