此题在卡码网109与力扣685题亦有记载 有一说一C#写法我没咋搞懂 就看明白了思路 这里贴一个答案待后续我醒悟了再来看罢
难就难在对整体数据结构classUnion(并查集)的理解不熟并且 对于输入输出这个迭代过程理解上也比较吃力
109. 冗余连接II
题目描述
有一种有向树,该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图:
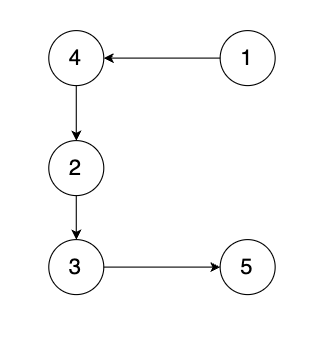
现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:

输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
输入描述
第一行输入一个整数 N,表示有向图中节点和边的个数。
后续 N 行,每行输入两个整数 s 和 t,代表这是 s 节点连接并指向 t 节点的单向边
输出描述
输出一条可以删除的边,若有多条边可以删除,请输出标准输入中最后出现的一条边。
输入示例
3
1 2
1 3
2 3输出示例
2 3提示信息
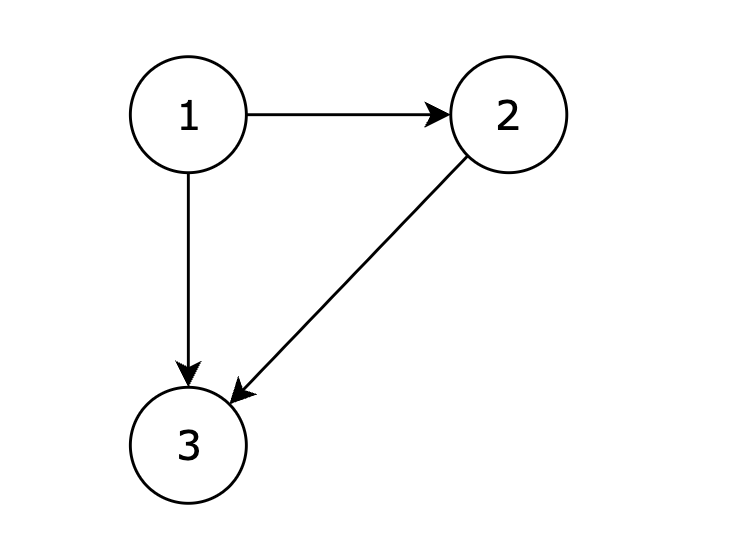
在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
数据范围:
1 <= N <= 1000.
思路:
//三种情况 情况一:如果我们找到入度为2的点,那么删一条指向该节点的边就行了
//入度为2 还有一种情况,情况二,只能删特定的一条边 ,如果发现入度为2的节点,我们需要判断 删除哪一条边,删除后本图能成为有向树。如果是删哪个都可以,优先删顺序靠后的边。
//情况三: 如果没有入度为2的点,说明 图中有环了(注意是有向环)解决方法:删掉构成环的边就可以了
//具体方法:前两种入度为2的情况,一定是删除指向入度为2的节点的两条边其中的一条,如果删了一条,判断这个图是一个树,那么这条边就是答案。同时注意要从后向前遍历,因为如果两条边删哪一条都可以成为树,就删最后那一条
//明确没有入度为2的情况,那么一定有向环,找到构成环的边就是要删除的边。
//解决本题要实现两个最为关键的函数:
//isTreeAfterRemoveEdge() 判断删一个边之后是不是有向树
//getRemoveEdge() 确定图中一定有了有向环,那么要找到需要删除的那条边
具体代码:
using System;
using System.Collections.Generic;
class Program
{
static int n;
static int[] father = new int[1001]; // 并查集的父节点数组
static List<Tuple<int, int>> edges = new List<Tuple<int, int>>(); // 边的列表
static int[] inDegree; // 记录节点入度
// 并查集初始化
static void Init()
{
for (int i = 1; i <= n; ++i)
{
father[i] = i;
}
}
// 并查集里寻根的过程
static int Find(int u)
{
if (u == father[u])
return u;
return father[u] = Find(father[u]);
}
// 将v->u 这条边加入并查集
static void Join(int u, int v)
{
u = Find(u);
v = Find(v);
if (u != v)
{
father[v] = u;
}
}
// 判断u和v是否在同一个集合中
static bool Same(int u, int v)
{
return Find(u) == Find(v);
}
// 在有向图里找到删除的那条边,使其变成树
static void GetRemoveEdge(List<Tuple<int, int>> edges)
{
Init(); // 初始化并查集
foreach (var edge in edges)
{
int u = edge.Item1;
int v = edge.Item2;
if (Same(u, v)) // 构成有向环了,就是要删除的边
{
Console.WriteLine($"{u} {v}");
return;
}
else
{
Join(u, v);
}
}
}
// 删一条边之后判断是不是树
static bool IsTreeAfterRemoveEdge(List<Tuple<int, int>> edges, int deleteEdge)
{
Init(); // 初始化并查集
for (int i = 0; i < n; i++)
{
if (i == deleteEdge) continue;
int u = edges[i].Item1;
int v = edges[i].Item2;
if (Same(u, v)) // 构成有向环了,一定不是树
{
return false;
}
Join(u, v);
}
return true;
}
static void Main()
{
// 读入数据
n = int.Parse(Console.ReadLine());
inDegree = new int[n + 1]; // 记录节点入度
for (int i = 0; i < n; i++)
{
string[] input = Console.ReadLine().Split();
int s = int.Parse(input[0]);
int t = int.Parse(input[1]);
inDegree[t]++;
edges.Add(new Tuple<int, int>(s, t));
}
List<int> vec = new List<int>(); // 记录入度为2的边
// 找入度为2的节点所对应的边,注意要倒序,因为优先删除最后出现的一条边
for (int i = n - 1; i >= 0; i--)
{
if (inDegree[edges[i].Item2] == 2)
{
vec.Add(i);
}
}
// 情况一、情况二
if (vec.Count > 0)
{
// 放在vec里的边已经按照倒叙放的,所以这里就优先删vec[0]这条边
if (IsTreeAfterRemoveEdge(edges, vec[0]))
{
Console.WriteLine($"{edges[vec[0]].Item1} {edges[vec[0]].Item2}");
}
else
{
Console.WriteLine($"{edges[vec[1]].Item1} {edges[vec[1]].Item2}");
}
return;
}
// 处理情况三
// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
GetRemoveEdge(edges);
}
}





