我们知道，测试活动中充满了不确定性。我们测试人员都很喜欢缺陷，找到缺陷能给我们带来很多成就感。但是我们也经常碰到一些让我们深恶痛绝的缺陷。

这就是那些不能稳定复现的缺陷——我测的时候发现问题了，提了bug，开发修的时候来找了，说在我这儿试了，没问题啊，同样的数据，同样的环境。我说不可能，再试试，结果我们哥俩吭哧吭哧研究一下午，发现做50次才会出一次问题，你说坑不坑爹。不过这还算好的，至少我测的时候发现问题了，要是没发现，上线了才出问题，那就更惨了。做性能测试的时候，这种不确定性的表现就更明显了。同一个性能场景，重复做多次，响应时间每次都不一样。所以性能测试用的指标是平均响应时间，这就是借助了统计的手段。实际上，被测对象的质量特性，经常会表现出一定的随机性。要测试这样的特性，就需要依靠统计的思想。

另一方面，以质量评估为目标的测试，在大部分情境下表现为部分归纳推理。也就是依靠“一部分”测试输入点的测试结果，来推断被测对象在整个测试输入空间上的表现。

这种推理，有一个重要的特点，就是“结论有或然性”。我们在测试报告里给出的测试结论，一般都是“XX版本测试通过”。那“测试通过”到底意味着什么？意味着达到了公司的测试通过标准？那达到标准又意味着什么？意味着上线肯定不会出问题吗？显然不是。那退一步讲，意味着不会出三级以上的严重缺陷吗？肯定也不是。再退一步讲，意味着“测过”的功能就没问题了吗？好像也不能说的那么绝对。所以“测试通过”这个结论，看似掷地有声，实则言之无物；看似斩钉截铁，实则含混暧昧。那么，怎么才能得到一个比较科学、可靠、可信的测试结论呢？我们需要依靠统计的思想。

陈希孺院士说，统计不止是一种方法或技术，还含有世界观的成分——它是看待万事万物的一种视角。统计思想的核心，就是从随机性中探寻规律性，以此来认识和把握事物的本质特征——比如被测对象的质量特性。

为了后面讨论方便，我们首先需要复习一下数理统计的基础知识。在讨论多样化思想的时候，我们提到过一些历史上很著名的试验，比如孟德尔的豌豆杂交试验，伽利略的自由落体试验。还有一个名垂青史的试验，就是抛硬币。

抛硬币这个试验非常简单，但是很让人上头，很多大数学家都做过这个试验。为什么呢？因为这个试验有一种神秘的色彩，虽然每次抛硬币的结果是不确定的，有时候正面朝上，有时候反面朝上，是一种完全随机的现象，但只要抛的次数足够多，正面朝上发生的可能性就会稳定在50%上下，无论抛硬币的人是谁，在什么时间，什么地点。就好像冥冥中有一种力量，在控制着试验结果。

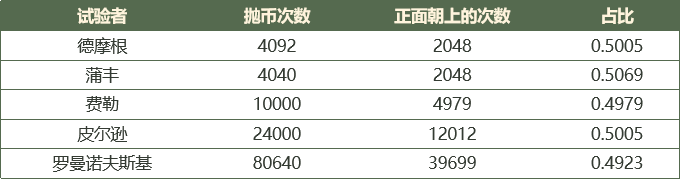
抛硬币这样的试验，我们叫做随机试验；抛硬币两种可能的结果：“正面朝上”、“反面朝上”，都叫做随机事件。随机事件之间常见的关系有：

  ①互斥，也就是“两个事件不可能同时发生”；

  ②互补，也就是“两个事件有且仅有一个会发生”；

  ③独立，也就是“一个事件发生与否，跟另一个事件完全没关系”。

比如，抛硬币“正面朝上”和“正面朝上”这两个随机事件，就是互斥、互补（如果不考虑硬币立着没倒的情况）的关系，但不是互相独立的关系。

随机事件发生的可能性大小，就是这个随机事件的概率。比如抛硬币正面朝上的概率，就是0.5。

如果把“正面朝上”记作1、“正面朝上”记作2，那么抛硬币的结果就是一个不确定的变量，取值可能是1，也可能是2。这就是随机变量。

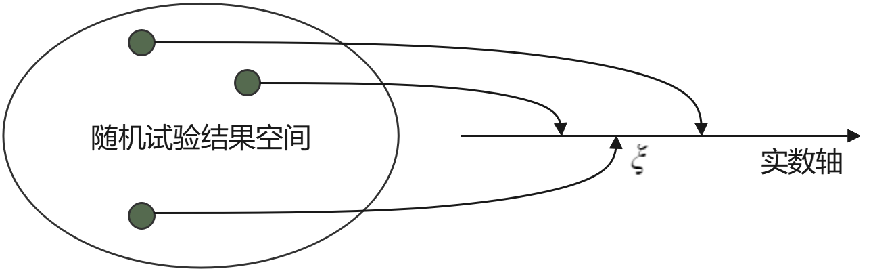
随机变量取各种值的可能性，叫做随机变量的概率分布。如果随机变量只能取有限个值，比如1和2，这种变量叫做离散型随机变量，离散型随机变量可以给每个取值定义概率大小；如果随机变量取值可以是任意实数，那就是连续型随机变量，这种变量我们没法说它“取某个值的概率是多少”，只能用概率分布累积函数，来说明它“取值在某个范围内的概率是多少”。概率分布累积函数又可以表示成概率分布密度函数的积分。一般我们用如下的概率分布密度函数曲线，来表征一个连续型随机变量的概率分布：

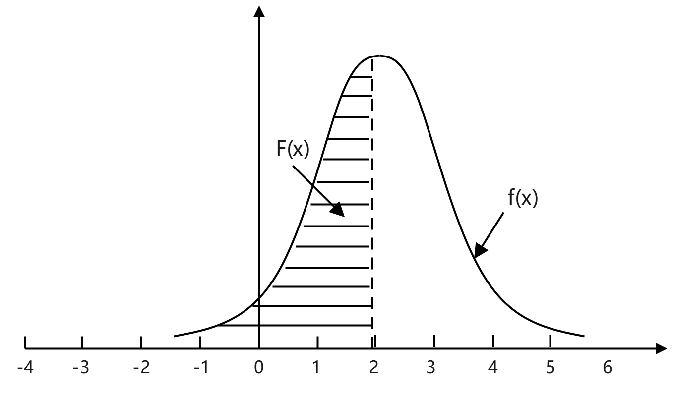
曲线和X轴围成的面积，就是“变量取值在某个范围内的概率”​。