矩阵是什么
矩阵就是二维数组,下面是一个 m 乘 n 的矩阵,它有 m 行,n 列,每行每列上面都有元素,每个元素都有行标i 和列标 j, a ij 。简称m × n矩阵,记作:
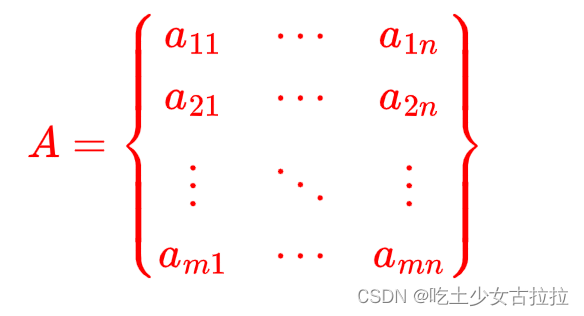
注意a11的索引是 A[0,0]。
这 m×n 个数称为矩阵 A 的元素,简称为元,数aij
位于矩阵 A 的第 i 行第 j 列,称为矩阵 A 的 (i,j) 元,m×n 矩阵 A 也记作 A mn 。
常见矩阵
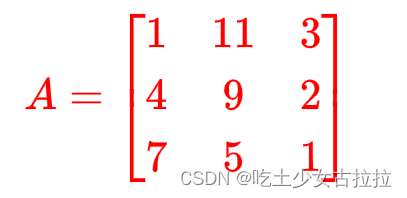
方阵
如果 m 等于 n,那就称为方阵
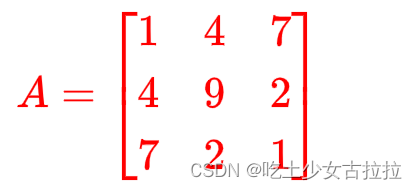
对称矩阵
定义是 a ij 等于 a ji 那么就是对称矩阵,对称矩阵首先是个方阵
单位矩阵
主对角线都是 1,其它位置是 0,这称之为单位矩阵,单位矩阵写为 I,一定是方阵,等同于数字里面的 1。

对角矩阵
对角矩阵,就是主对角线非 0,其它位置是 0。
 矩阵一定是方阵。不然没有对角线!" />
矩阵一定是方阵。不然没有对角线!" />
矩阵运算
矩阵加减法
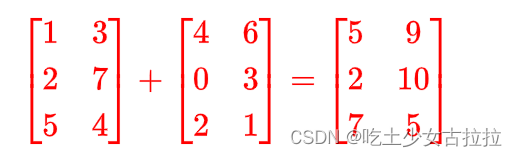
矩阵的加法就是矩阵的对应位置相加,减法也是一样就是对应位置相减。
数乘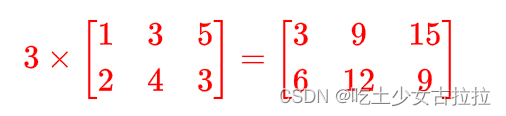
矩阵乘法
矩阵的乘法和一般的乘法是不太一样!
它是把第一个矩阵的每一行,和第二个矩阵的每一列拿过来做内积得到结果。
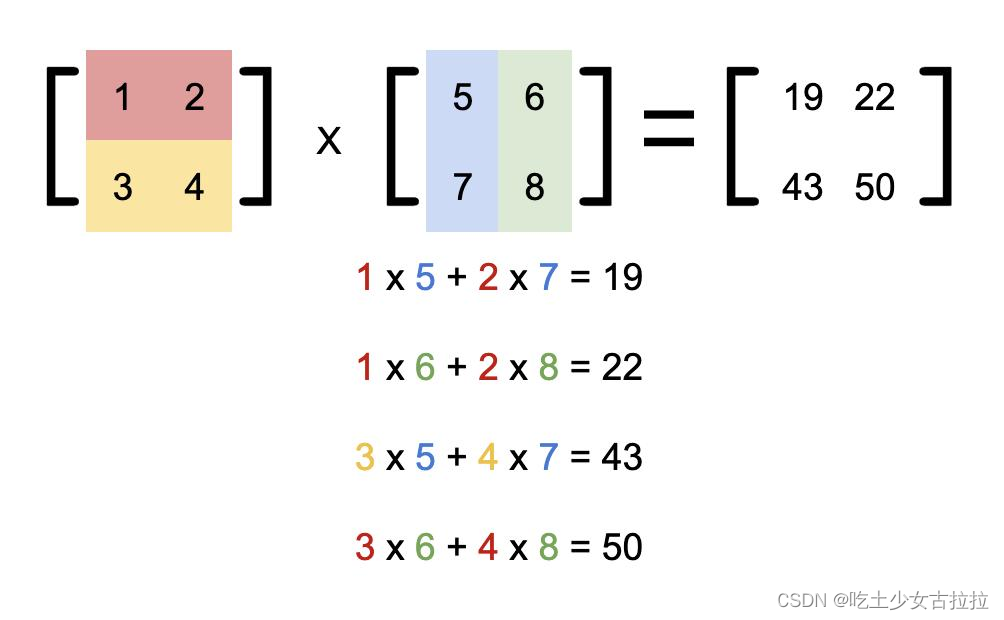
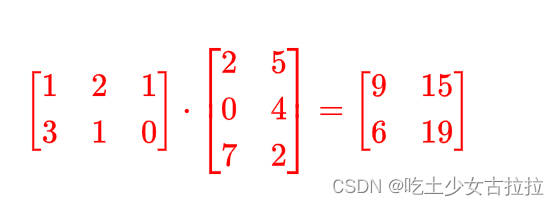
矩阵乘法运算结果
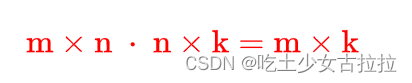
矩阵转置
转置的操作和向量是一样的,就是把 a ij变成 a ji ,把行和列互换一下

矩阵运算法则
矩阵加减法
满足:分配律、结合律、交换律
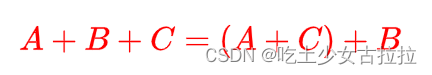
矩阵乘法
满足结合律
满足分配律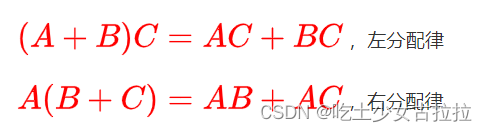
不满足交换律:不一定相等,甚至 AB 的尺寸和 BA 的尺寸是不同的。
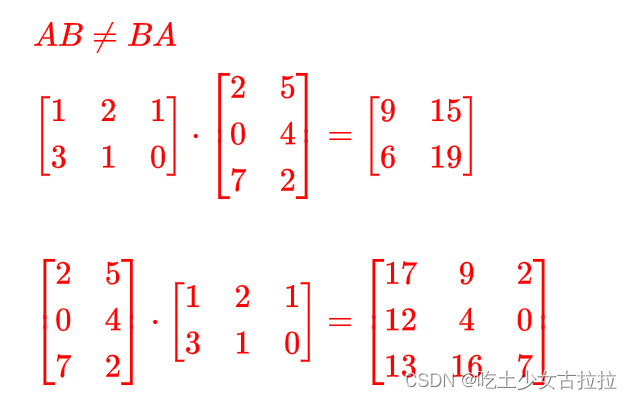
矩阵乘法 + 转置
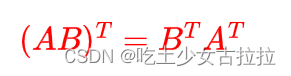
逆矩阵
逆矩阵定义
矩阵有 AB 乘法,但是没有 A/B 这么一说,只有逆矩阵。
逆矩阵怎么定义的?
假设有个矩阵 A,注意它一定是方阵(必须是方阵),乘以矩阵 B 等于单位矩阵I:
那么我们称这里的 B 为 A 的右逆矩阵,和左逆矩阵。
有个很重要的结论就是,如果这样的 B 存在的话,它的左逆和右逆一定相等,统称为 A 的逆矩阵 A −1 。则:A=B−1 B=A−1 (-1次方)
逆矩阵作用
矩阵求逆有什么用呢?它可以帮助我们解线性方程组,比如 XW=Y 。两边同时乘以 X 的逆: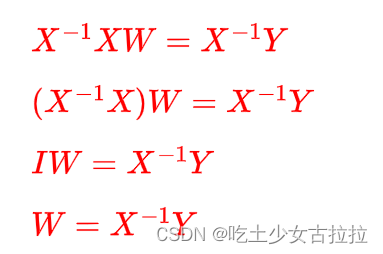
就可以求解出方程的系数,它发明的目的也是干这样的事情用的。
举例说明:
# 三元一次方程
# 3x + 2y + 4z = 19
# 2x -y + 3z = 9
# x + y - z = 0
import numpy as np
X = np.array([[3,2,4],[2,-1,3],[1,1,-1]])
Y = np.array([19,9,0])display(X,Y)# np.linalg.inv表示矩阵求逆
# dot表示矩阵乘法
W = np.linalg.inv(X).dot(Y)
print('求解方程得x,y,z为:',W)
'''
array([[ 3, 2, 4],[ 2, -1, 3],[ 1, 1, -1]])
array([19, 9, 0])
求解方程得x,y,z为: [1. 2. 3.]
'''
从这里我们也可以看出来单位矩阵像我们乘法里面的 1。
逆矩阵相关公式:
伴随矩阵
伴随矩阵定义
设有一矩阵 A
设 A ij 是矩阵A中元素 a ij 的代数余子式,那么矩阵 A ∗ 矩阵 A 的伴随矩阵" />
矩阵 A 的伴随矩阵" />
代数余子式
1、代数余子式定义
2、代数余子式计算
计算过程如下: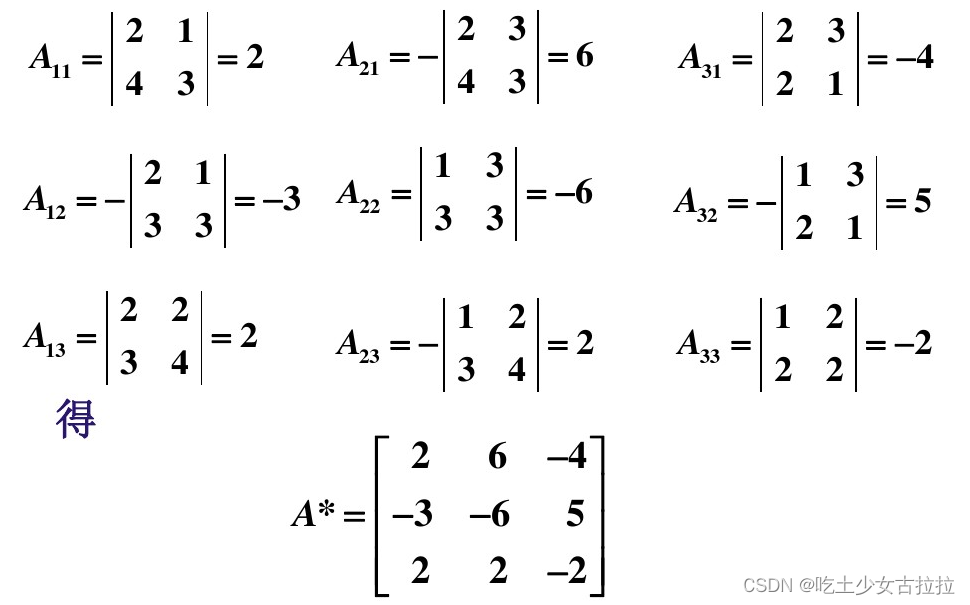
伴随矩阵性质 矩阵" />
矩阵" />
伴随矩阵与逆矩阵

根据上式可得:
import numpy as np
# 声明矩阵
A = np.array([[1,2,3],[2,2,1],[3,4,3]])
A_bs = [] # 伴随矩阵
n = 3 # A方阵的行、列数量
for i in range(n):for j in range(n):row = [0,1,2] # 行索引col = [0,1,2] # 列索引row.remove(i) # 去除行col.remove(j) # 去除列# 代数余子式A_ij = A[np.ix_(row,col)]A_bs.append(((-1)**(i+j)) * np.linalg.det(A_ij))
A_bs = np.array(A_bs).reshape(3,3).T
print('根据伴随矩阵求逆矩阵:\n',A_bs/np.linalg.det(A))
print('用NumPy模块求逆矩阵 :\n',np.linalg.inv(A))
'''
根据伴随矩阵求逆矩阵:[[ 1. 3. -2. ][-1.5 -3. 2.5][ 1. 1. -1. ]]
用NumPy模块求逆矩阵 :[[ 1. 3. -2. ][-1.5 -3. 2.5][ 1. 1. -1. ]]
'''