描述
你是一个经验丰富的小偷,准备偷沿街的一排房间,每个房间都存有一定的现金,为了防止被发现,你不能偷相邻的两家,即,如果偷了第一家,就不能再偷第二家;如果偷了第二家,那么就不能偷第一家和第三家。
给定一个整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额。
数据范围:数组长度满足 1≤n≤2×105,数组中每个值满足 1≤num[i]≤5000
示例1
输入:
[1,2,3,4]
返回值:
6
说明:
最优方案是偷第 2,4 个房间
示例2
输入:
[1,3,6]
返回值:
7
说明:
最优方案是偷第 1,3个房间
示例3
输入:
[2,10,5]
返回值:
10
说明:
最优方案是偷第 2 个房间
思路分析:
该题使用动态规划来解决,
具体做法:
- step 1:用dp[i]表示长度为i的数组,最多能偷取到多少钱,只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。
- step 2:(初始状态) 如果数组长度为1,只有一家人,肯定是把这家人偷了,收益最大,因此dp[1]=nums[0]。
- step 3:(状态转移) 每次对于一个人家,我们选择偷他或者不偷他,如果我们选择偷那么前一家必定不能偷,因此累加的上上级的最多收益,同理如果选择不偷他,那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度,在nums中为下标。
图示:
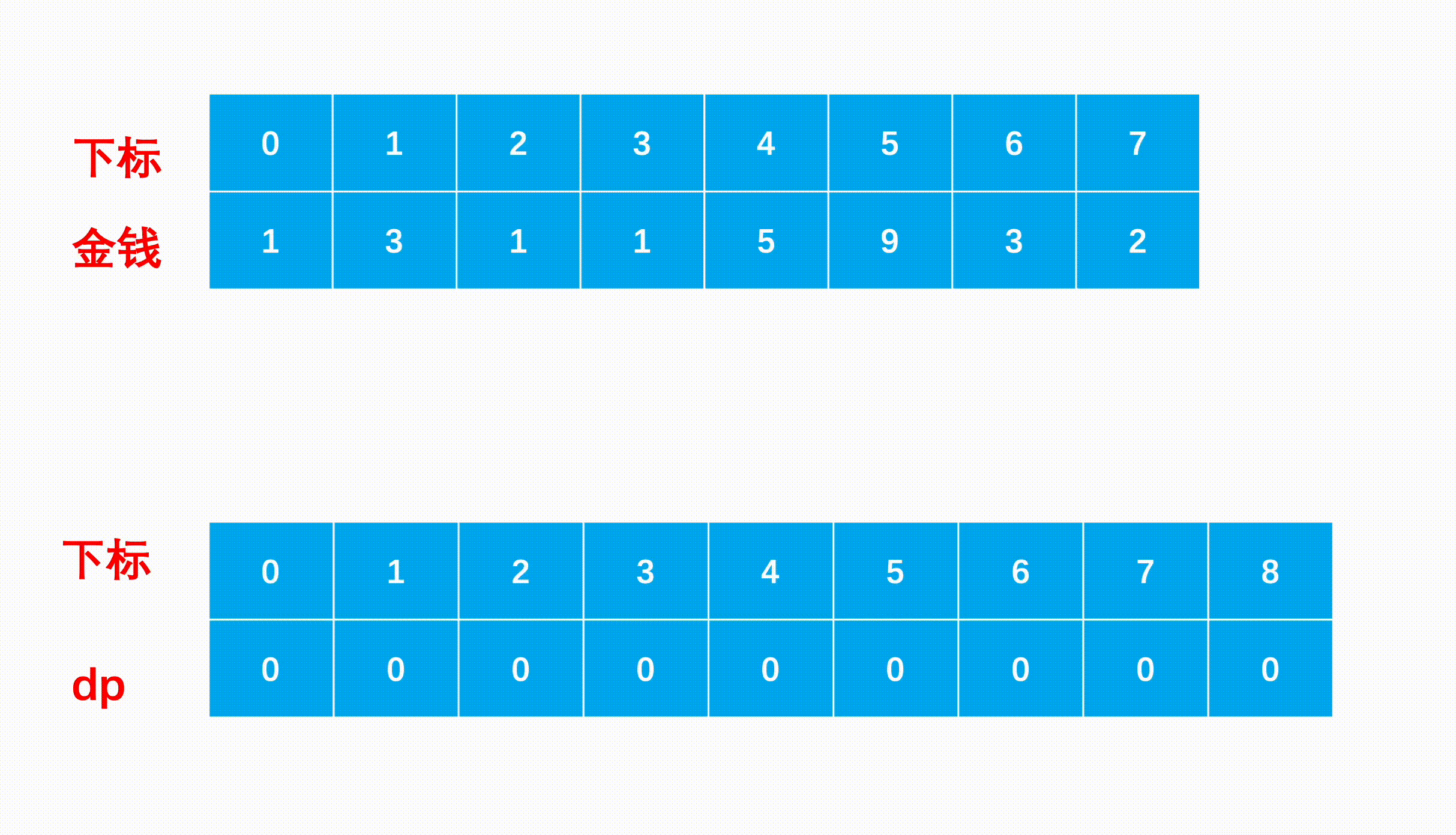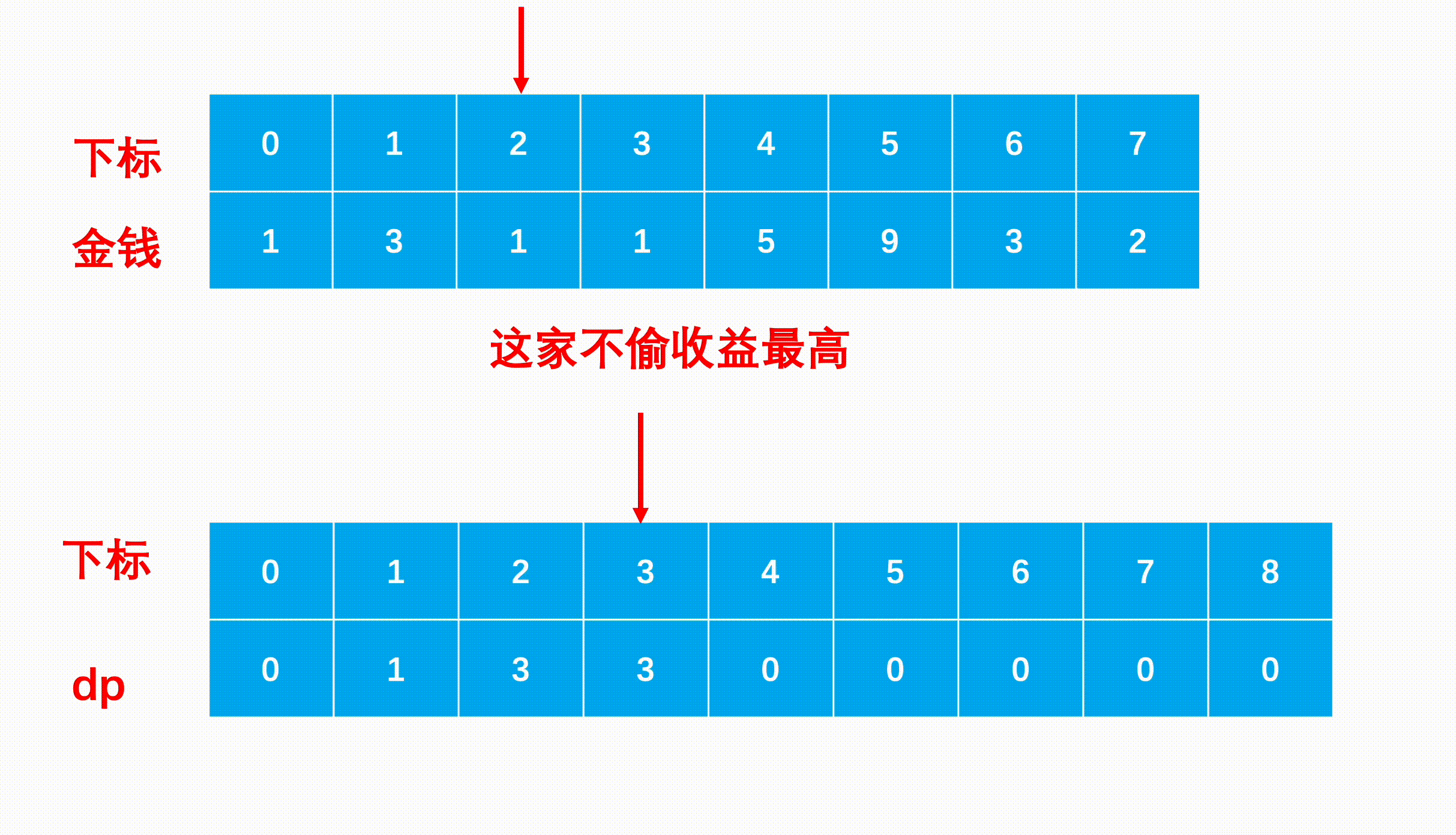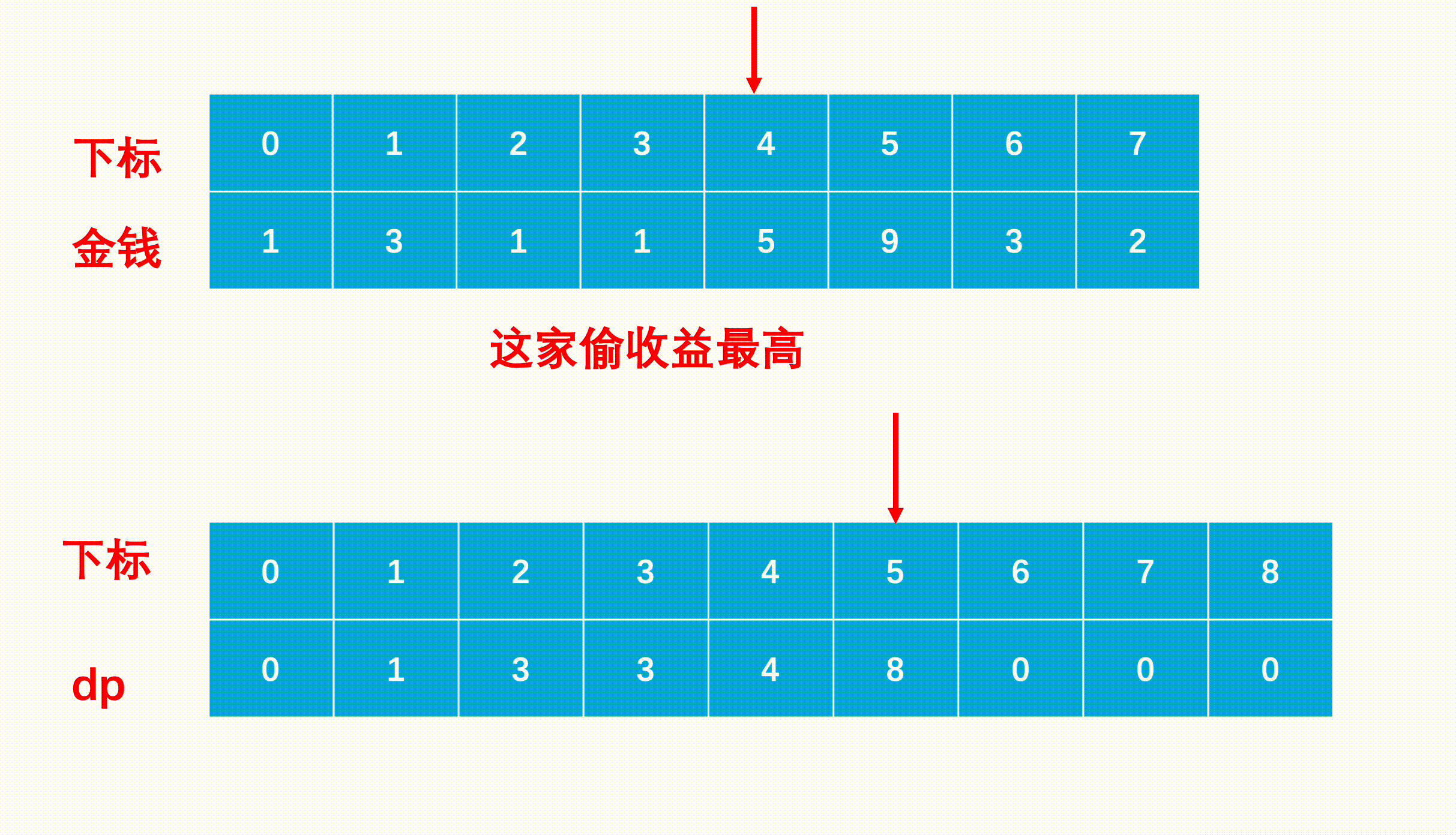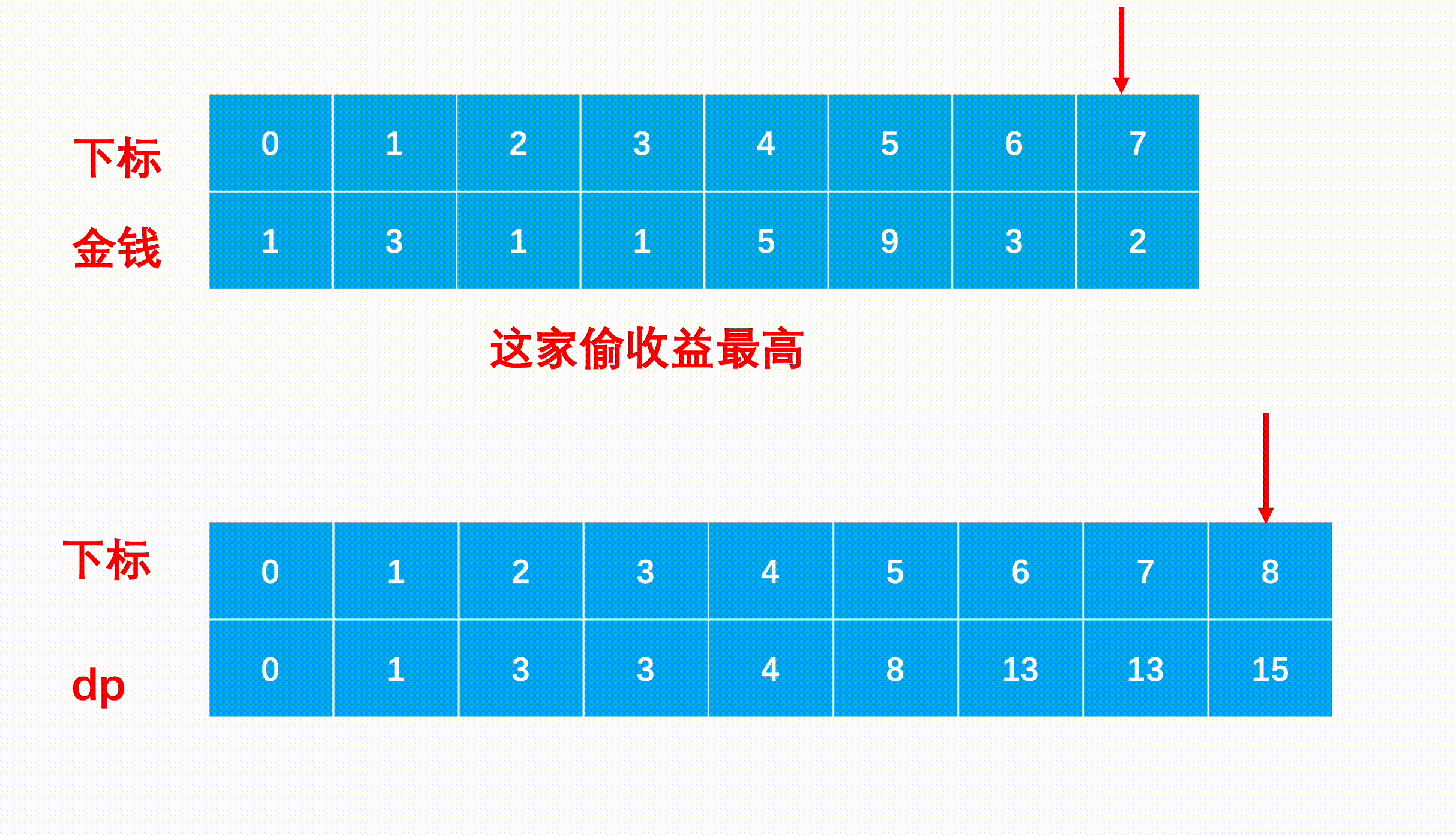
代码:
java">import java.util.*;public class Solution {/*** @param nums int整型一维数组 * @return int整型*/public int rob (int[] nums) {int[] dp=new int[nums.length+1];dp[1]=nums[0];for(int i=2;i<=nums.length;i++){dp[i]=Math.max(dp[i-1],nums[i-1]+dp[i-2]);}return dp[nums.length];}
}