相关文章
Cocos Creator UICanvas详解与2D游戏配置详解
前言
Cocos Creator是一款强大的2D游戏开发引擎,提供了丰富的工具和组件来帮助开发者快速制作出优秀的游戏作品。其中,UICanvas是Cocos Creator中一个非常重要的组件,用于管理游戏中的UI界面。
在本文中,我们将深入探讨Cocos Cr…
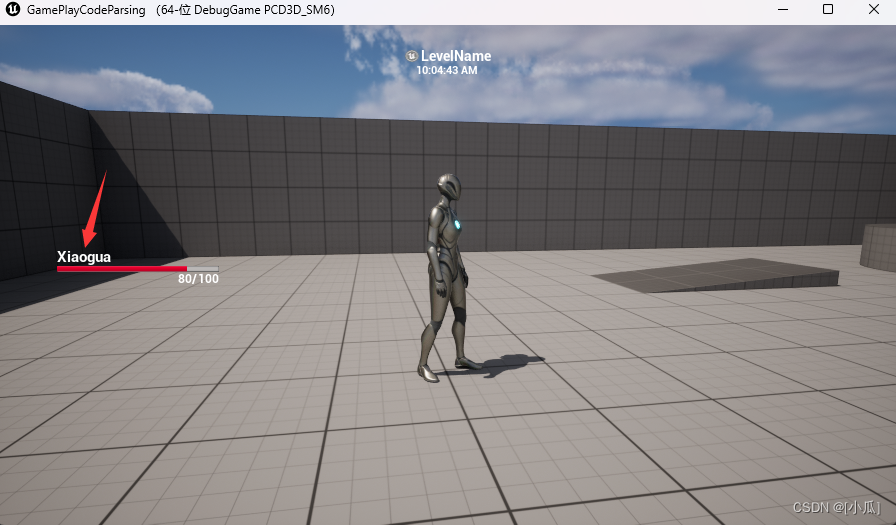
虚幻引擎5 Gameplay框架(二)
Gameplay重要类及重要功能使用方法(一)
配置LOG类及PlayerController的网络机制
探索验证GamePlay重要函数、类的执行顺序与含义
我们定义自己的日志,专门建立一个存放自己日志的类,这个类继承自BlueprintFunctionLibrary 然后…
uniapp 应用闪退、崩溃异常日志捕获插件(可对接网络上报)插件 Ba-Crash
应用闪退、崩溃异常日志捕获插件(可对接网络上报) Ba-Crash
简介(下载地址)
Ba-Crash 是一款uniapp应用闪退、崩溃异常日志捕获插件,支持对接网络上报、设置提示等等,方便对一些远程问题、原生问题进行分…
“Postman 中文版使用教程:如何切换到中文界面?”
Postman 的很好用的接口测试软件。但是,Postman 默认是英文版的,也不支持在软件内切换为中文版。很多同学的英语并不是很好,看到一堆的英文很是头痛。
今天我们来介绍下:切换到 Postman 中文版的方法。想要学习更多的关于 Postma…
在STM32上实现无线传感器网络节点
引言
无线传感器网络(WSN)是物联网(IoT)技术的关键组成部分,广泛应用于环境监测、智能建筑、精密农业等领域。
本教程将介绍如何在STM32微控制器上设计和实现一个无线传感器网络节点,包括硬件选择、网络协…
如何提升通信芯片一次性投片成功率
通信芯片设计是一个非常复杂的系统工程,整体流程设计包括产品定义,算法开发,架构设计,电路设计和验证,后端版图设计,晶圆生产到封装测试等多个环节。在每个环节中,都需要严格遵循设计规则和流程…
[Unity实战]热更新如何预防过度裁剪
情景再现
假设你现在有一个游戏客户端,客户端只打包了入口场景,游戏场景都存放在了AB包。
你打的热更包里使用了协程中的waituntil修复游戏场景中空投补给资源加载时机问题,但是打出来的热更在真机跑报如下错误:
TypeLoadExcep…
inout参数模式存储过程和删除查看存储过程和MySQL小总结
inout参数模式存储过程和删除查看存储过程
案例
传入a和b两个数,然后让a和b都乘以2后返回
create procedure myp7(inout a int , inout b int)
begin
set aa*2;
set bb*2;
end $
调用
set a10$set b20$call myp5(a,b)$select a,b $
删除存储过程
drop procedure 存储过程…