标签：栈
题意：给定$n$个球，第$i$个球的大小是$2^{a_i}$。轮流将这$n$个球加到一个序列中，一开始序列为空。每加一个球，如果序列的最后一个球和倒数第二个球大小相同，就将这两个球移除，然后加入一个新球，新球的大小是这两个球大小之和。不断地进行操作直到序列最后两个球不同或者序列中只有一个球了停止，然后再不断地加入球，直到这$n$个球都被加入了。求最后序列中剩下的球的个数。
题解：我们分析下样例，比如以下这个样例：
7
2 1 1 3 5 3 3
加入到第 3 个球的时候，形成 2 1 1，最后两个相同了，删掉这两个，然后加入一个 2，形成 2 2；最后两个又相同了，删掉这两个，然后加入一个 3。
加入第 4 个球的时候，形成 3 3，最后两个相同了，删掉这两个，然后加入一个 4，形成 4。
加入第 5 个球，形成 4 5。
加入第 6、7 个球，形成 4 5 3 3，最后两个相同了，删掉最后两个，加入一个 4。
所以最后序列中剩下 4 5 4。
注意：题目中输入的是球的指数，如果两个球大小相同都是$2^{a_i}$，那么相加就是$2\ast 2^{a_i}=2^{a_{i+1}}$。
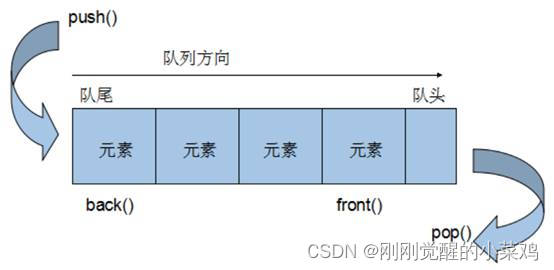
我们可以通过 栈 模拟不断地将最后的两个拿出来，然后进行合并，塞一个新的放到栈中的这个流程，不断进行这个操作，直到最后球都放完了，最终输出栈的大小即可。
代码：

#include <bits/stdc++.h>
using namespace std;stack<int> s;
int n, x;int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> x;s.push(x);while (s.size() >= 2) {int a = s.top(); s.pop();int b = s.top(); s.pop();if (a != b) {s.push(b);s.push(a);break;} else {s.push(a + 1);}}}cout << s.size() << endl;return 0;
}