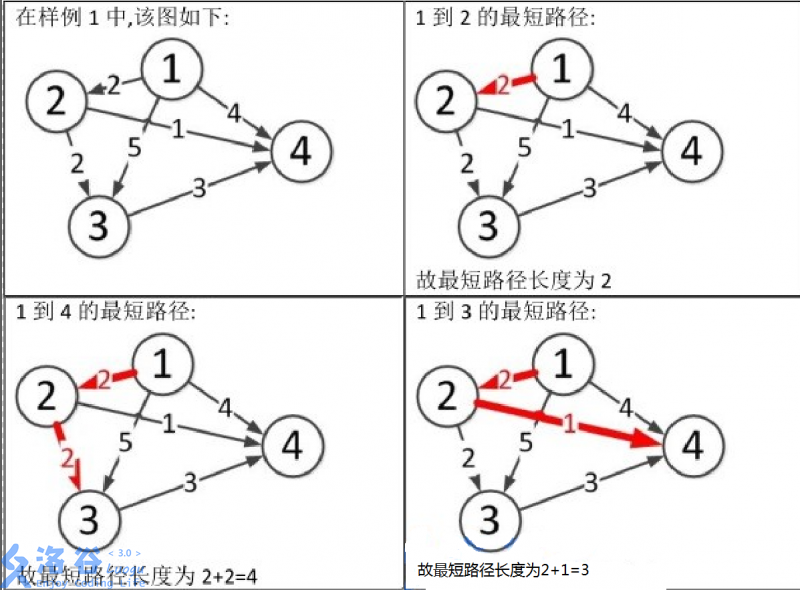
2005高教社杯全国大学生数学建模竞赛题目B
随着信息时代的到来，网络成为人们生活中越来越不可或缺的元素之一。许多网站利用其强大的资源和知名度，面向其会员群提供日益专业化和便捷化的服务。例如，音像制品的在线租赁就是一种可行的服务。这项服务充分发挥了网络的诸多优势，包括传播范围广泛、直达核心消费群、强烈的互动性、感官性强、成本相对低廉等，为顾客提供更为周到的服务。
考虑如下的在线DVD租赁问题。顾客缴纳一定数量的月费成为会员，订购DVD租赁服务。会员对哪些DVD有兴趣，只要在线提交订单，网站就会通过快递的方式尽可能满足要求。会员提交的订单包括多张DVD，这些DVD是基于其偏爱程度排序的。网站会根据手头现有的DVD数量和会员的订单进行分发。每个会员每个月租赁次数不得超过2次，每次获得3张DVD。会员看完3张DVD之后，只需要将DVD放进网站提供的信封里寄回（邮费由网站承担），就可以继续下次租赁。请考虑以下问题：

1）网站正准备购买一些新的DVD，通过问卷调查1000个会员，得到了愿意观看这些DVD的人数（表1给出了其中5种DVD的数据）。此外，历史数据显示，60%的会员每月租赁DVD两次，而另外的40%只租一次。假设网站现有10万个会员，对表1中的每种DVD来说，应该至少准备多少张，才能保证希望看到该DVD的会员中至少50%在一个月内能够看到该DVD？如果要求保证在三个月内至少95%的会员能够看到该DVD呢？
2）表2中列出了网站手上100种DVD的现有张数和当前需要处理的1000位会员的在线订单（表2的数据格式示例如下表2），如何对这些DVD进行分配，才能使会员获得最大的满意度？请具体列出前30位会员（即C0001~C0030）分别获得哪些DVD。
3）继续考虑表2，并假设表2中DVD的现有数量全部为0。如果你是网站经营管理人员，你如何决定每种DVD的购买量，以及如何对这些DVD进行分配，才能使一个月内95%的会员得到他想看的DVD，并且满意度最大？
4）如果你是网站经营管理人员，你觉得在DVD的需求预测、购买和分配中还有哪些重要问题值得研究？请明确提出你的问题，并尝试建立相应的数学模型。

表1 对1000个会员调查的部分结果

DVD名称	DVD1	DVD2	DVD3	DVD4	DVD5
愿意观看的人数	200	100	50	25	10

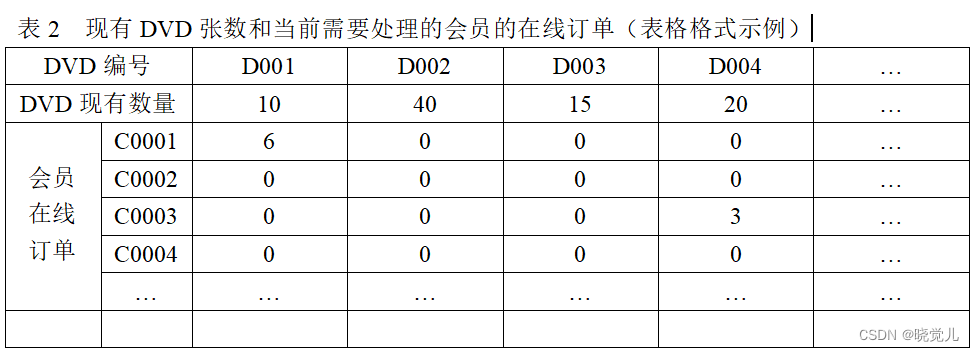
注：D001~D100表示100种DVD, C0001~C1000表示1000个会员, 会员的在线订单用数字1,2,…表示，数字越小表示会员的偏爱程度越高，数字0表示对应的DVD当前不在会员的在线订单中。
（注：表2数据位于文件B2005Table2.xls中）

question1

question1.1

建立租赁模型:
设有$x$张DVD，想看会员数为两万，满足度为$50\%$
有$a\%$个会员租赁两次，$(1-a)\%$个会员租赁一次
可得：$2\ast x\ast a\%+x\ast (1-a)\%=20000\ast 0.5$
根据题目可知$a=60$
解得$x=6250$

将模型一般化，设统计中愿意观看的人数为$b$,满足度为$w$,则想看会员数为$b/1000\ast 100000$
$x=\lceil (b/1000\ast 100000\ast w)/(2\ast a\%+(1-a\%))\rceil$

DVD名称	DVD1	DVD2	DVD3	DVD4	DVD5
愿意观看的人数	200	100	50	25	10
需要准备张数	6250	3125	1563	782	313

question1.2 如果要求保证在三个月内至少95%的会员能够看到该DVD呢？

以下模型建立在租两次的会员月初租赁，月末还 ， 租一次的会员月初租，下月初还

建立会员重复模型：
设第$i$个月来的会员数为$y_i$个会员
每个月有$a\%$个会员租赁两次，$(1-a)\%$个会员租赁一次，$a=60$
设会员重复率为$C\%$ , $C=50$
则其中$\min (a\%y_j\ast C\%,a\%y_i\ast C\%)$和是同一个会员
其中$\min ((1-a)\%y_j\ast C\%,(1-a)\%y_i\ast C\%)$和是同一个会员

引入question1.1的模型
设统计中愿意观看的人数为$b$,满足度为$w$,则想看会员数为$b/1000\ast 100000$

设第$i$个月有$x$张DVD
有$a\%$个会员租赁两次，$(1-a)\%$个会员租赁一次
第$i$个月来的满足的会员数为$y_i$个会员
可得：$2\ast x_i\ast a\%+x_i\ast (1-a)\%=y_i$

来的会员总数减去重复会员数必须大于等于要满足的会员数
$\{\begin{array}{l}{y}_1+y_2+y_3-\min (a\%y_2\ast C\%,a\%y_1\ast C\%)-\min (a\%y_3\ast C\%,a\%y_2\ast C\%)-\min (a\%y_1\ast C\%,a\%y_3\ast C\%)-\min ((1-a)\%y_2\ast C\%,(1-a)\%y_1\ast C\%)-\min ((1-a)\%y_3\ast C\%,(1-a)\%y_2\ast C\%)-\min ((1-a)\%y_1\ast C\%,(1-a)\%y_3\ast C\%)\ge b/1000\ast 100000\ast w\\ 2\ast x_i\ast a\%+x_i\ast (1-a)\%=y_i,i=1,2,3\\ ans=min(x_1+x_2+x_3)\end{array}$

question2

设变量$x_{ij}$为租赁给第$i$个会员第$j$种DVD的情况，设定$x_{ij}=1$为租，$x_{ij}=0$为不租
如果有$n$个客户,$m$种DVD,客户在线订单数为$orde{r}_{ij}$
则单个会员满意量为$b_{ij}=\{\begin{array}{l}(11-orde{r}_{ij}),orde{r}_{ij}>0\\ 0,orde{r}_{ij}=0\end{array}$
那么客户总满意度量:$\max ans={\sum }_{1\le i\le n,1\le j\le m}{x}_{ij}\ast b_{ij}$

要保证DVD数量不能超标
设第$j$种DVD有$su{m}_j$个，题目已知$su{m}_j$
${\sum }_{1\le i\le n}{x}_{ij}<=su{m}_j,j=1,2,\mathrm{3....},m$

每个客户发3张不同的DVD或者不发DVD：
设0/1变量 $y_i$
${\sum }_{1\le j\le m}{x}_{ij}=y_i\ast 3,i=1,2,3,..n$

需要保证每个人都不会收到自己不喜欢的DVD，即客户在线订单数为0时候，不可以租给他。
$x_{ij}\le orde{r}_{ij},i=1,2,3,..n,j=1,2,3,..m$

LINGO求解：

lingo">sets:aa/1..1000/:y;bb/1..100/:sum;cc(aa,bb):order,x,b;
endsets
data:
order = @ole('D:\homewrok\建模\DVD租赁\B2005Table2.xls','order');
sum = @ole('D:\homewrok\建模\DVD租赁\B2005Table2.xls','dvdsumj');
enddata@for(cc(i,j):b(i,j)=@if(order(i,j)#gt#0,11-order(i,j),0));
max=@sum(cc(i,j):x(i,j)*b(i,j));
@for(bb(j):@sum(aa(i):x(i,j))<=sum(j));
@for(aa(i):@sum(bb(j):x(i,j))=y(i)*3);
@for(cc(i,j):x(i,j)<=order(i,j));
@for(cc(i,j):@bin(x(i,j)));
@for(aa(i):@bin(y(i)));

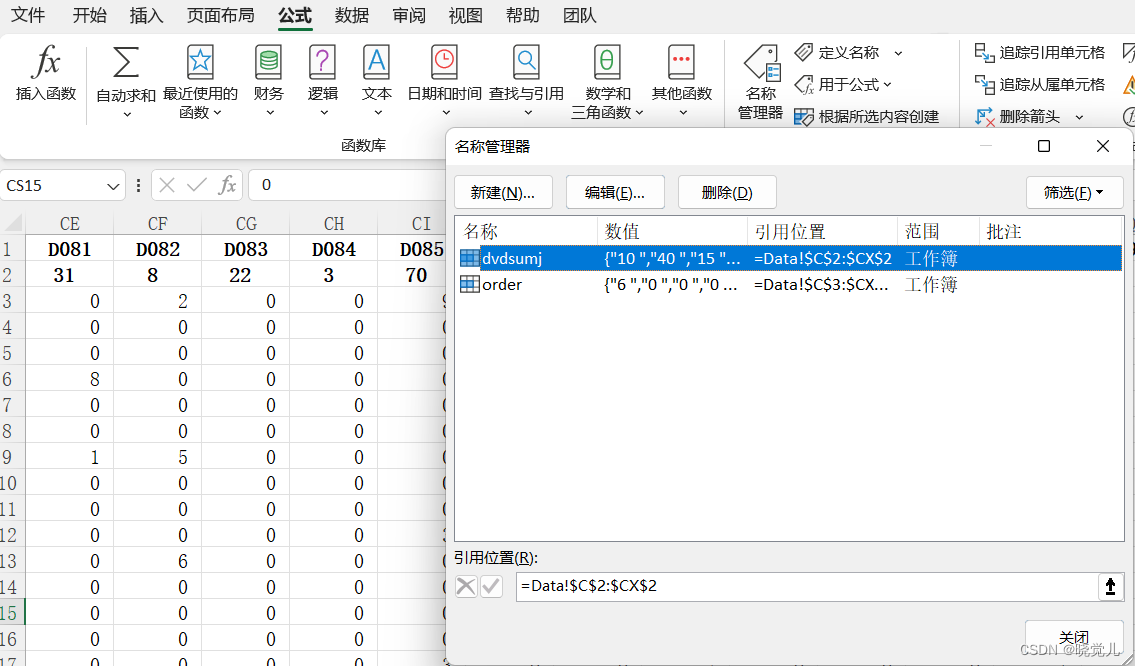
注：LINGO读取EXCEL方法

客户/DVD ID	第一张	第二张	第三张
C0001	D008	D041	D098
C0002	D006	D044	D062
C0003	D032	D050	D080
C0004	D007	D018	D041
C0005	D011	D066	D068
C0006	D019	D053	D066
C0007	D026	D066	D081
C0009	D053	D078	D100
C0010	D041	D055	D085
C0011	D059	D063	D066
C0012	D002	D031	D041
C0013	D021	D078	D096
C0014	D023	D052	D089
C0015	D013	D052	D085
C0016	D010	D084	D097
C0017	D047	D051	D067
C0018	D041	D060	D078
C0019	D066	D084	D086
C0020	D045	D061	D089
C0021	D045	D050	D053
C0022	D038	D055	D057
C0023	D029	D041	D095
C0024	D037	D041	D076
C0025	D009	D069	D081
C0026	D022	D068	D095
C0027	D050	D058	D078
C0028	D008	D034	D082
C0029	D026	D030	D055
C0030	D037	D062	D098

question3

在满足第二问的模型下:注意:$su{m}_j$是变量(未知)

$\{\begin{array}{l}{b}_{ij}=\{\begin{array}{l}(11-orde{r}_{ij}),orde{r}_{ij}>0\\ 0,orde{r}_{ij}=0\end{array}\\ \max ans={\sum }_{1\le i\le n,1\le j\le m}{x}_{ij}\ast b_{ij}\\ {\sum }_{1\le i\le n}{x}_{ij}<=su{m}_j,j=1,2,\mathrm{3....},m\\ {\sum }_{1\le j\le m}{x}_{ij}=y_i\ast 3,i=1,2,3,..n\\ x_{ij}\le orde{r}_{ij},i=1,2,3,..n,j=1,2,3,..m\end{array}$

因为$su{m}_j$是变量,我们决定每种DVD的购买量,需要满足DVD总量不变,设已知总量为$nu{m}_{sum}$
${\sum }_{1\le j\le m}su{m}_j=nu{m}_{sum}$

要使一个月内95%的会员得到他想看的DVD,按照第二问的限制下即发三张DVD就是满足该客户，否则不满足
${\sum }_{1\le i\le n}{y}_i\ge n\ast 95\%$

再加上要使一个月内95%的会员得到他想看的DVD(舍弃)
${\sum }_{1\le i\le n}({\sum }_{1\le j\le m}(orde{r}_{ij}!=0)={\sum }_{1\le j\le m}{x}_{ij}\ast (orde{r}_{ij}!=0))\ge n\ast 95\%$

LINGO求解：

lingo">sets:aa/1..1000/:y;bb/1..100/:sum,num;cc(aa,bb):order,x,b;
endsets
data:
order = @ole('D:\homewrok\建模\DVD租赁\B2005Table2.xls','order');
num = @ole('D:\homewrok\建模\DVD租赁\B2005Table2.xls','dvdsumj');
enddata@for(cc(i,j):b(i,j)=@if(order(i,j)#gt#0,11-order(i,j),0));
max=@sum(cc(i,j):x(i,j)*b(i,j));
@for(bb(j):@sum(aa(i):x(i,j))<=sum(j));
@for(aa(i):@sum(bb(j):x(i,j))=y(i)*3);
@for(cc(i,j):x(i,j)<=order(i,j));
@sum(bb(j):sum(j))=@sum(bb(j):num(j));
@sum(aa(i):y(i))>=950;
@for(cc(i,j):@bin(x(i,j)));
@for(aa(i):@bin(y(i)));