在学习数据结构前,我们需要了解时间复杂度和空间复杂度的概念,这能够帮助我们了解数据结构。
算法效率分为时间效率和空间效率
时间复杂度
一个算法的复杂度与其执行的次数成正比。算法中执行基础操作的次数,为算法的时间复杂度。
我们采用大O的渐进表示法。
推导大O阶方法:
1用常数1取代运行时间中的所有加法常数
2在修改后的运行次数函数中,保留最高阶项。
3如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
在实际中一般情况关注的是算法的最坏运行情况
举例:
冒泡排序的时间复杂度

 从这个例子我们知道了,不是一层循环时间复杂度就是N,两层就是N^2要看具体算法实现。
从这个例子我们知道了,不是一层循环时间复杂度就是N,两层就是N^2要看具体算法实现。
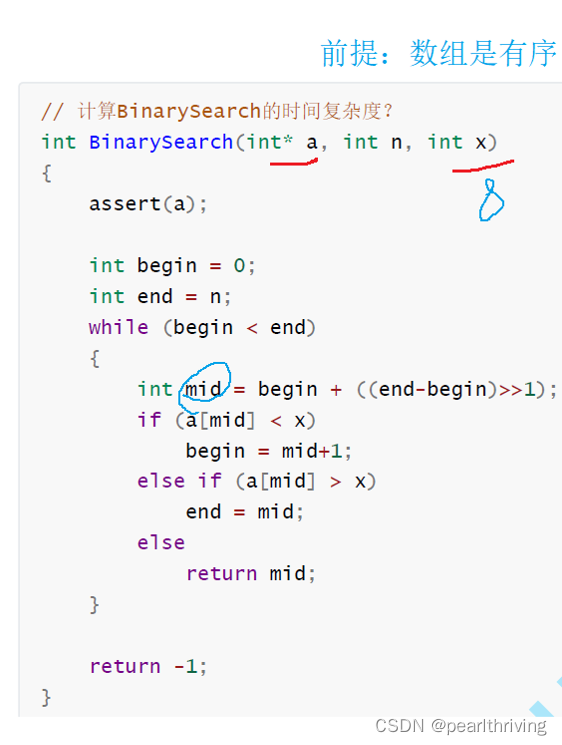
二分法时间复杂度分析:

 阶乘递归的时间复杂度
阶乘递归的时间复杂度

 空间复杂度
空间复杂度
对临时储存空间占用大小的量度。计算的是变量的个数。
首先来看冒泡排序的时间复杂度

循环走了N次,重复利用的是一个空间。
斐波那契数列的空间复杂度:
 阶乘的时间复杂度:
阶乘的时间复杂度: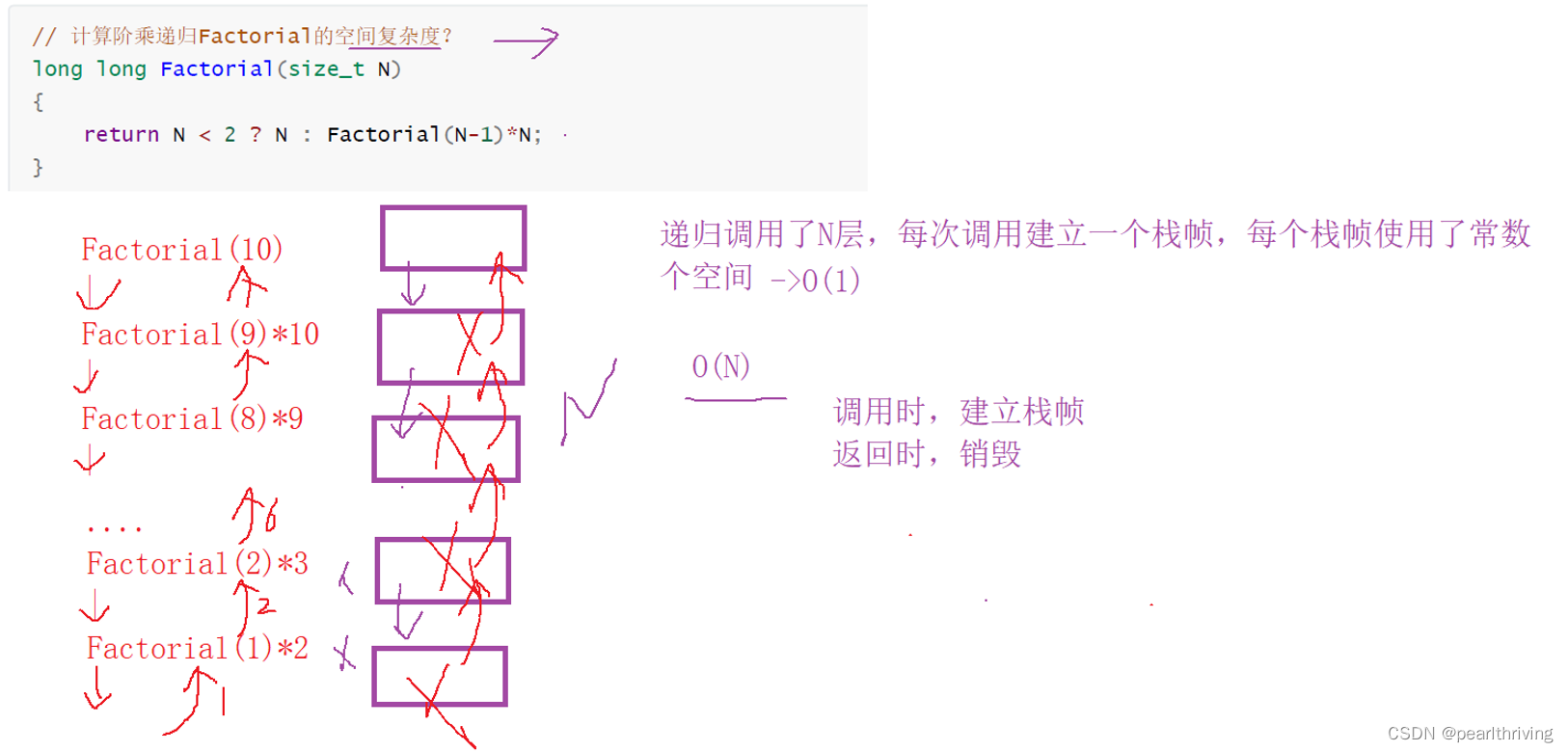
算法题
消失的数字
面试题 17.04. 消失的数字 - 力扣(LeetCode)
思路1:
排序,如果后一个数字不等于前一个数字加1,那么前一个数字加1,就是要寻找的消失的数字。
这种方法的时间复杂度是N*lgN
思路2:
把0到N加起来,再减去各个数字,得到的数字就是消失的数字。这里的时间复杂度是O(N)。如果先累加,时间复杂度是0(N),依次遍历一遍为O(N)。
int missingNumber(int* nums, int numsSize){int N=numsSize;int ret=(0+N)*(N+1)/2;for(int i=0;i<numsSize;++i){ret-=nums[i];}return ret;}
思路3:
把数组中的所有数字跟0到N异或,剩下的数字就是消失的数字。(我们知道,x^x=0,0^x=x)
int missingNumber(int* nums, int numsSize){int N=numsSize;int x=0;for(int i=0;i<numsSize;i++){x^=nums[i];//x将包含数组nums中所有元素的异或结果}for(int j=0;j<=N;j++){x^=j;}return x;}
189. 轮转数组 - 力扣(LeetCode)
思路1:旋转k次
void rotate(int* nums, int numsSize, int k) {//首先把最后一个数储存起来for(int i=0;i<k;i++){int tmp=nums[numsSize-1];for(int i=numsSize-2;i>=0;i--){nums[i+1]=nums[i];}nums[0]=tmp;}
}思路2:三段逆置
前k个逆置
后k个逆置
再整体逆置
void Reverse(int*nums,int left,int right)
{while(left<right){int tmp=nums[left];nums[left]=nums[right];nums[right]=tmp;left++;right--;}
}
void rotate(int* nums, int numsSize, int k)
{if(k>=numsSize){k%=numsSize;}Reverse(nums,numsSize-k,numsSize-1);Reverse(nums,0,numsSize-k-1);Reverse(nums,0,numsSize-1);
}思路3:
以空间换时间

void _rotate(int*nums,int numsSize,int k,int*tmp)
{k%=numsSize;int n=numsSize;memcpy(tmp,nums+n-k,sizeof(int)*k);//将数组最后 k 个元素复制到 tmp 数组的前 k 个位置memcpy(tmp+k,nums,sizeof(int)*(n-k));//将数组的前 (n-k) 个元素复制到 tmp 数组的剩余位置 memcpy(nums,tmp,sizeof(int)*(n));// // 将 tmp 数组的内容复制回 nums 数组
}
void rotate(int* nums, int numsSize, int k)
{int tmp[numsSize];_rotate(nums,numsSize,k,tmp);
}