一、说明
在概率和统计学中,了解结果是如何量化的至关重要。概率质量函数 (PMF) 和概率密度函数 (PDF) 是实现此目的的基本工具,每个函数都提供不同类型的数据:离散和连续数据。
二、PMF 的定义:
概率质量函数 (PMF) 表示离散随机变量的概率分布,该变量可以具有有限或可数无限数量的可能值。它有助于量化每种可能结果的确切概率。
如果 X 是一个离散随机变量,那么它的范围 R_X 是一个可数集,因此,我们可以列出 R_X 中的元素。换句话说,我们可以写:
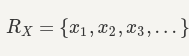
请注意,这里是 x1、x2、x3,...是随机变量 X 的可能值。虽然随机变量通常用大写字母表示,但表示范围内的数字,我们通常使用小写字母,例如 x、x1、y、z 等来表示可能的值。对于离散随机变量 X,我们感兴趣的是知道 X=x_k 的概率。
请注意,此处事件 A={X=x_k} 定义为样本空间 S 中 X 的相应值等于 x_k 的结果集 s。
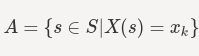
事件 {X=x_k} 的概率由 X 的概率质量函数 (PMF) 正式表示。
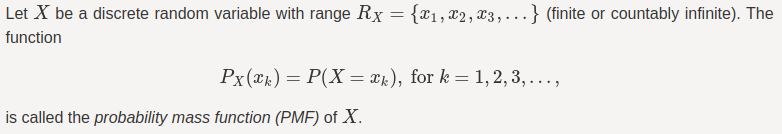
PX(1) 显示 X=1 的概率
- PMF 的特性:
- PMF 始终为非负值:所有 PMF 均≥ 0(x_i x_i
- 所有概率之和为 1: ∑i P(X = x_i) = 1
2. 与 PDF 的比较:
- PMF 用于离散随机变量,而 PDF 用于连续随机变量。
- PMF 在离散点处对概率求和,而 PDF 在一个范围内积分。
3. 解释 PMF 值:
- 特定点的 PMF 值 x_i 表示概率 P(X = x_i)
4. 图形表示:
- 绘制 PMF 涉及绘制每个离散结果的概率,通常使用条形图。
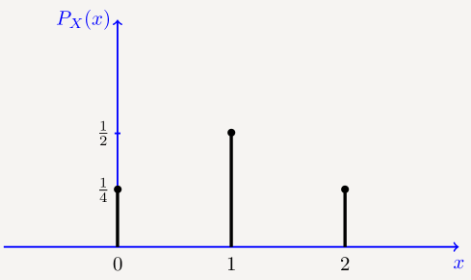
图 1.随机变量 X 的 PMF 的图形表示
5. 意思是:
离散随机变量 X 的期望值表示为 E[X],计算为 X 可以采用的所有可能值的加权平均值,其中权重对应于这些值发生的概率,离散随机变量 X 的期望值由以下公式给出:
![]()
例如,如果我们有一个随机变量 X,它可以取值 1、2 和 3,概率分别为 P(X=1) = 0.1、P(X=2) = 0.4 和 P(X=3) = 0.5,那么 X 的期望值将计算为:
E[X] = 1*0.1 + 2*0.4 + 3*0.5 = 1 + 0.8 + 1.5 = 2.4
大数定律 (LLN)
- 大数定律指出,随着试验或实验次数的增加,结果的平均值将趋向于向预期值收敛。换句话说,您进行的试验或实验越多,样本均值就越接近真实总体均值。
- 大数定律最早由 Gerolamo Cardano 提及。雅各布·伯努利 (Jacob Bernoulli) 证明了二元随机变量的这种定律的特殊形式(他花了 20 多年时间才开发出足够严格的数学证明)。他将此命名为“黄金定理”,但它后来被普遍称为“伯努利定理”。这不应与以雅各布·伯努利的侄子丹尼尔·伯努利命名的伯努利原则相混淆。后来泊松将其描述为“la loi des grands nombres”(“大数定律”)。
在这段代码中,我想用 Python 代码演示,通过模拟大量试验来演示大数定律。
import randomdef calculate_sample_mean(num_trials):total_outcomes = 0for _ in range(num_trials):# a random variable with values 1 to 6outcome = random.randint(1, 6) total_outcomes += outcomesample_mean = total_outcomes / num_trialsreturn sample_mean# Define the expected value for comparison
expected_value = 3.5# Test the Law of Large Numbers with increasing number of trials
for num_trials in [10, 50, 100, 1000, 10000, 100000]:sample_mean = calculate_sample_mean(num_trials)print(f"Number of trials: {num_trials}, Sample mean: {sample_mean}, Expected value: {expected_value}")这是上述代码的输出,通过将不同次数的试验的样本平均值与预期值(在本例中为 3.5)进行比较来检验大数定律:

随着试验次数的增加,样本均值应收敛于预期值
6. 方差和标准差公式
离散随机变量 X 的方差度量 X(随机变量)的分布围绕其预期值的分布。有两个主要公式用于计算随机变量 X 的方差:
公式 1:使用期望的方差:
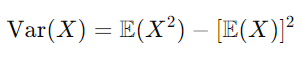
此公式根据随机变量的期望值 (平均值) 和平方的期望值来表示方差。它派生如下:

公式 2:使用概率和平均值的方差:
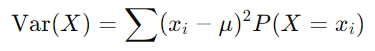
其中 μ = E(X)
此公式通过将 X 的每个可能值与平均值之间的平方差相加来计算方差,并按每个值的概率加权。它主要用于结果数量有限的离散随机变量:
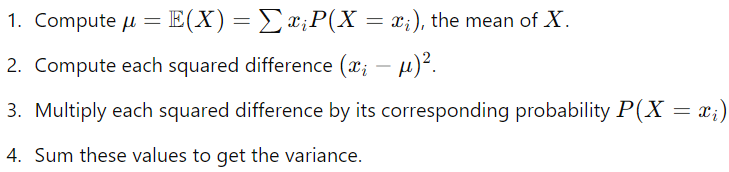
标准差:
标准差只是方差的平方根。它是以与原始数据相同的单位衡量离散度的指标,使其更易于解释。
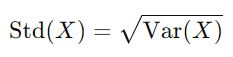
三、以两种方式计算 Variance 的示例
考虑具有以下概率分布的离散随机变量 X:
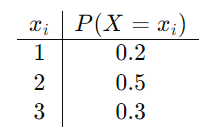
使用两个公式的分步计算:
- 计算均值μ:
![]()
2. 公式 1:使用期望的方差
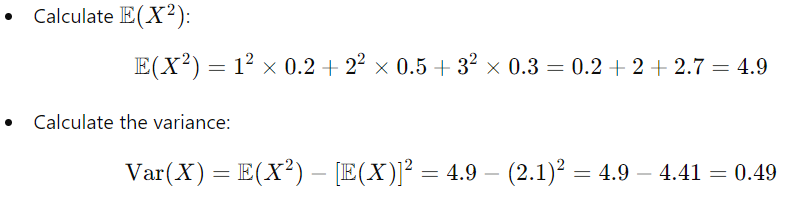
3. 公式 2:使用概率和平均值的方差
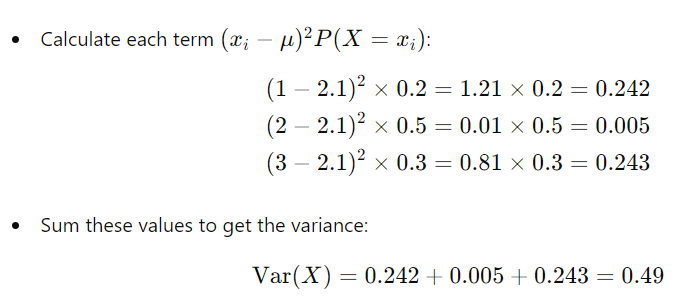
要找到标准差 (Std(X)),您只需取方差的平方根 (Var(X))
鉴于:
![]()
您可以按如下方式找到标准差:
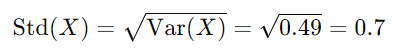
例
简单的 Python 代码,演示如何计算给定数据集的平均值、方差和标准差并打印结果。
import numpy as np# Sample data
data = [10, 12, 15, 18, 20, 22, 25, 28, 30, 32]# Calculate mean
mean = np.mean(data)# Calculate variance
variance = np.var(data)# Calculate standard deviation
std_deviation = np.sqrt(variance)# Print the results
print(f"Mean: {mean}")
print(f"Variance: {variance}")
print(f"Standard Deviation: {std_deviation:.3}")# Mean: 21.2
# Variance: 51.56
# Standard Deviation: 7.18四、示例 PMF (粉末动力学):
例如,考虑掷一个公平的六面骰子。PMF 为每个结果(1、2、3、4、5 和 6)分配 1/6 的概率,因为每个面都有相同的机会正面朝上着陆。这种情况的 PMF 为每个结果分配了 1/6 的概率,因为每个数字出现的机会相同。
表格: 掷出公平的六面骰子的概率分布
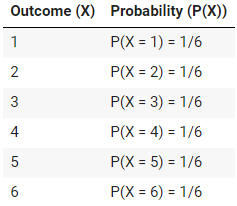
此表清楚地说明了 PMF 如何在掷骰子的所有可能结果中分配概率,确保总概率总和为 1。公式 P(X = x) = 1/6 表示每个结果 x(其中 x 为 1、2、3、4、5 或 6)的概率相等,为 1/6。
概率密度函数 (PDF):
概率密度函数 (PDF) 描述了连续随机变量具有特定值的可能性。与离散概率不同,任何特定点的 PDF 值都不是概率,而是密度。
PMF 不适用于连续随机变量,因为对于连续随机变量,所有 x ∈ R 为 P(X=x)=0。相反,我们通常可以定义概率密度函数 (PDF)。PDF 是概率密度,而不是概率质量。这个概念与物理学中的质量密度非常相似:它的单位是每单位长度的概率。要了解 PDF,请考虑一个连续随机变量 X,并按如下方式定义函数 fX(x)(只要存在限制):
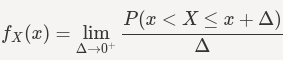
函数 fX(x) 为我们提供了点 x 处的概率密度。它是区间概率的极限 (x, x+Δ] 除以区间长度,当区间长度变为 0 时。请记住
![]()
因此,我们得出结论:
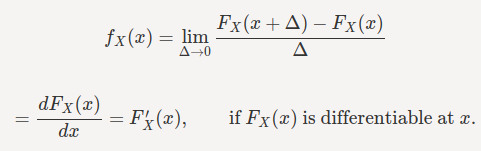
因此,我们对连续随机变量的 PDF 有以下定义:

- PDF 的属性:
- PDF 始终为非负数:f(x)≥0 表示所有 x
- 整个范围内 PDF 曲线下的面积为 1:
![]()
2. 解释 PDF 值:
- PDF 在任何点的高度都表示概率的密度,而不是实际概率。
- 要查找随机变量落在特定范围内的概率,请在该范围内对 PDF 进行积分。
3. 图形表示:
- 绘制 PDF 图形有助于可视化数据的分布。
- 重要的是要突出显示两点之间曲线下的面积,它表示变量落在该范围内的概率。
图 2 显示了 X 的 PDF。正如我们所看到的,PDF 的值在从 a 到 b 的区间内是恒定的。这就是为什么我们说 X 均匀分布在 [a,b] 上。
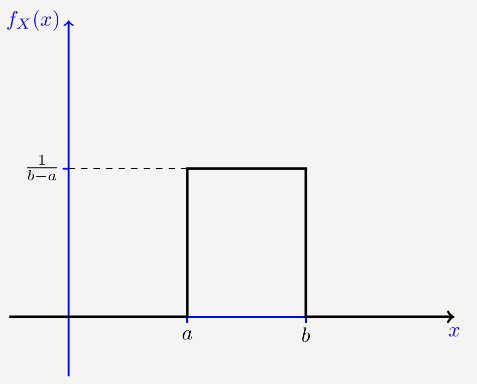
图 2.均匀分布在 [a,b] 上的连续随机变量的 PDF
4. 均值和方差:
- 连续随机变量的平均值(期望值)为:
![]()
- 差异为:
![]()
五、结论
第 19 天,我们探讨了概率质量函数 (PMF) 和概率密度函数 (PDF) 的核心概念。这些函数对于理解如何将概率分别分配给离散随机变量和连续随机变量至关重要。




