【R语言实战】——多模型预测及评价

🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972

个人介绍: 研一｜统计学｜干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项，参与研究经费10w、40w级横向

文章目录

1 项目任务
2 数据集介绍
3 加载相关包并读取数据
4 探索和准备数据
5 划分训练集和测试集
6 拟合最小二乘线性回归模型
7 拟合岭回归模型
8 拟合LASSO模型
9 拟合 PCR 模型
10 拟合PLS模型
11 模型评估
12 完整代码

该篇文章主要展示了利用R语言建立最小二乘线性回归、岭回归、LASSO、PCR、PLS五种模型对“College”数据集中的申请数量进行预测，并进行模型评估。

1 项目任务

使用“College”数据集中的其他变量预测收到的申请数量。

(a)将数据集分成训练集和测试集。

(b)在训练集上使用最小二乘法拟合线性模型，并报告所获得的测试误差。

©在训练集上拟合岭回归模型，通过交叉验证选择 λ。报告获得的测试误差。

(d)在训练集上拟合 LASSO 模型，通过交叉验证选择 λ。报告获得的测试误差，以及非零系数估计值的数量。

(e)在训练集上拟合 PCR 模型，通过交叉验证选择 M。报告获得的测试误差，以及通过交叉验证选择的 M 值。

(f)在训练集上拟合 PLS 模型，通过交叉验证选择 M。报告获得的测试误差，以及通过交叉验证选择的 M 值。

(g)对获得的结果进行评论。我们能多准确地预测收到的大学申请数量？这五种方法产生的测试误差有很大差别吗？

2 数据集介绍

这个数据集包含了大量关于不同学校的详细数据，主要变量包括： 1.Private：是否为私立学校。 2.Apps：申请人数。 3.Accept：被录取人数。 4.Enroll：注册人数。 5.Top10perc：排名前 10%的新生比例。 6.Top25perc：排名前 25%的新生比例。 7.F.Undergrad：全职本科生人数。 8.P.Undergrad：兼职本科生人数。 9.Outstate：州外学费。 10.Room.Board：房间和伙食费用。 11.Books：书籍费用。 12.Personal：个人费用。 13.PhD：拥有博士学位的教师比例。 14.Terminal：教师拥有终极学位的比例。 15.S.F.Ratio：学生与教师的比例。 16.perc.alumn：捐赠的校友比例。 17.Expend：学生教育支出。 18.Grad.Rate：毕业率。此外，该数据集还公布了学校名称。

3 加载相关包并读取数据

运行程序：

library("class")  
library("caret") 
library("gmodels") 
library('pls')
data<- read.csv("D:\\机器学习与R语言\\College.csv",header = T)
head(data)     #查看前六行

运行结果：

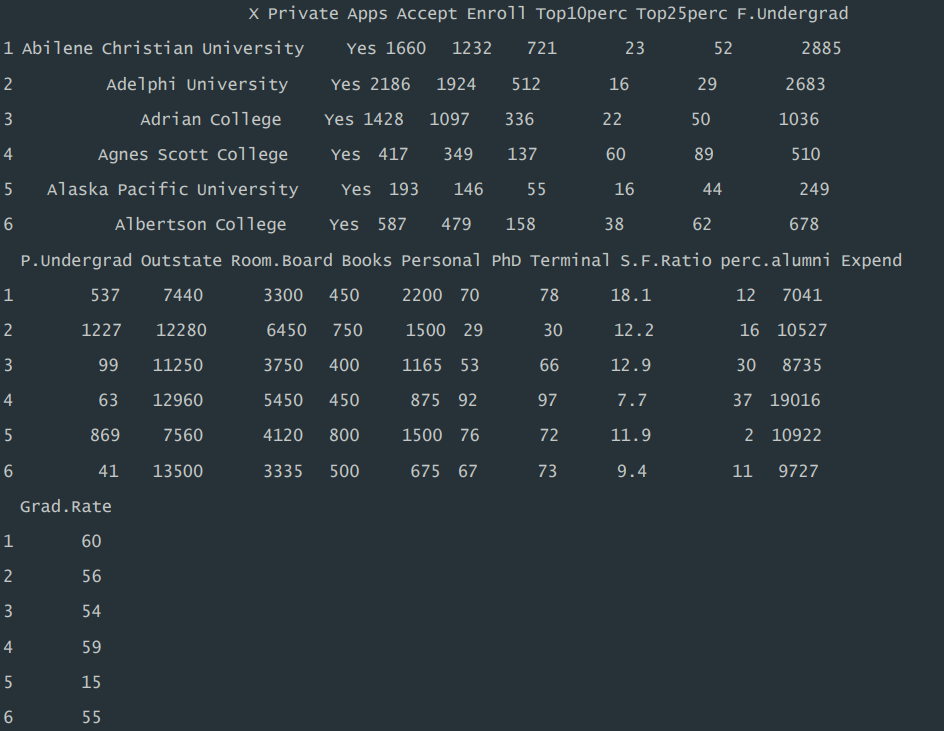
4 探索和准备数据

1）使用 str()发现，该数据集共有 777 个观测值，19 个属性，同时，其涉及的数据类型有字符型（int）和整型（int），其中“Apps”为目标变量。

运行程序：

str(data)                       #查看数据类型

运行结果：

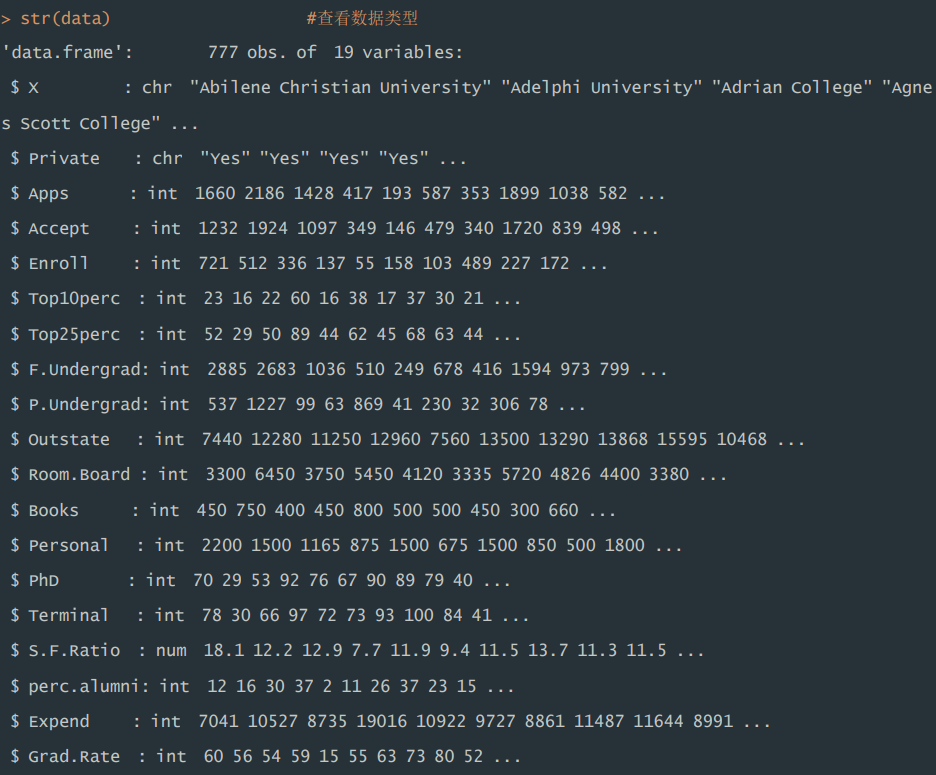
2）使用 table（）函数输出数据集中“Private”变量分布情况，同时利用 ifelse （）函数将其转化为 0-1 变量，其中“Yes”转化为 1，“No”转化为 0。该数据集中，私立学校和公立学校数量分别为 565、212。

运行程序：

table(data$Private)
data$Private_Yes=ifelse(data$Private=="Yes",1,0) #将分类变量Private转化为0-1变量，保存为Private_Yes
data=data[c(1,3:20)]                            ##剔除字符变量Private

运行结果：

3）利用 summary（）查看各变量数据特征情况，见运行结果，包括每个特征的最小值，1/4 分位数，中位数，均值，3/4 分位数，最大值。其中“Apps”数量分布在 81-48094 之间。

运行程序：

data<-data[c('Apps','Accept','Enroll','Top10perc','Top25perc','F.Undergrad','P.Undergrad','Outstate','Room.Board','Books','Personal','PhD','Terminal','S.F.Ratio','perc.alumni','Expend','Grad.Rate','Private_Yes')]summary(data)

运行结果：

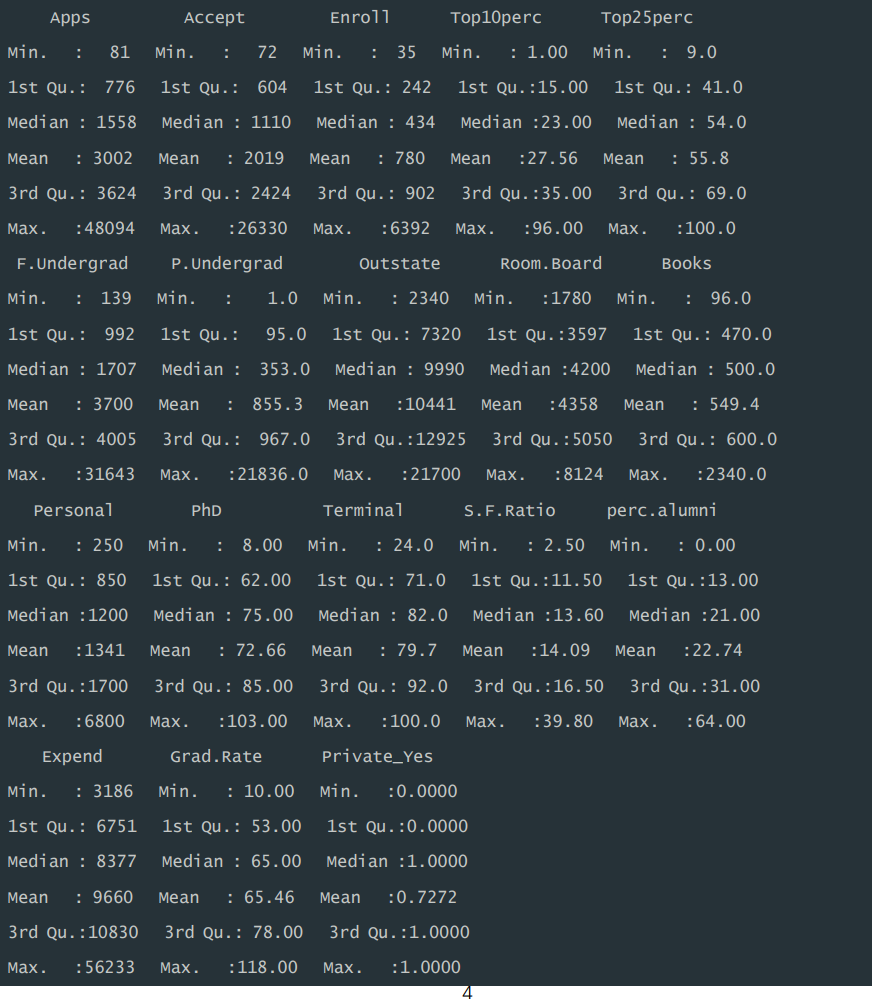
5 划分训练集和测试集

运行程序：

set.seed(123) #设置随机种子以保证结果可重复
trainIndex=createDataPartition(data$Apps,p=0.8,list=FALSE,times=1)data_train<-data[trainIndex, ] #创建训练集
data_test<-data[-trainIndex, ] #创建测试集

6 拟合最小二乘线性回归模型

1）模型总结。训练集中，根据运行结果显示，线性回归方程 F 值为 537.3， p 值远小于 0.05，说明拟合的回归方程在 0.05 的显著性水平上显著成立。拟合优度 R 2 为 0.9378，说明申请数量有 93.78%的信息可以用模型中的自变量来解释，模型效果较好。其中，变量“Accept”、“Enroll”、“Top10perc”、“Top25perc”、 “F.Undergrad”、“Outstate”、“Expend”、“Grad.Rate”、“Private_Yes”在 0.05 的显著性水平下，对因变量“Apps”存在显著影响。

运行程序：

lm_model=lm(Apps~.,data=data_train) #拟合线性回归模型
summary(lm_model)

运行结果：

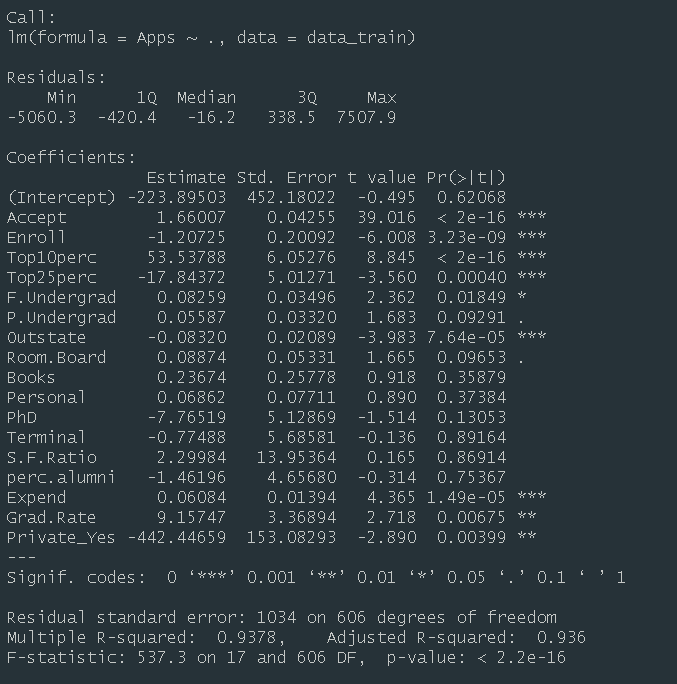
2）测试误差。根据运行结果显示，最小二乘线性回归模型，在测试集表现中，RMSE 为 1106.46，MAE 为 609.14。

运行程序：

lm_pred=predict(lm_model,newdata=data_test) #对测试集进行预测
lm_error_RMSE=sqrt(mean((lm_pred-data_test$Apps)^2)) #计算均方根误差
lm_error_MAE=mean(abs(lm_pred-data_test$Apps)) #计算绝对平均误差print(paste("线性模型测试误差RMSE:",lm_error_RMSE))
print(paste("线性模型测试误差MAE:",lm_error_MAE))

运行结果：

7 拟合岭回归模型

1）模型总结。训练集中，在拟合岭回归模型过程中，利用交叉验证的方式选择最优正则化λ，根据结果运行显示，对应最小 MSE 的λ值为 388.9，MSE 为1785806，在该 λ 值下，模型中非零系数的数量为 17（不包含截距项），且在最小 MSE 的一个标准误差内的最大 λ 值为 1430.4，MSE 为 2405994，该 λ 值下，模型中非零系数的数量为 17（不包含截距项）。

运行程序：

ridge_model=cv.glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps,alpha=0) #交叉验证拟合岭回归模型
print(ridge_model) #输出模型

运行结果：

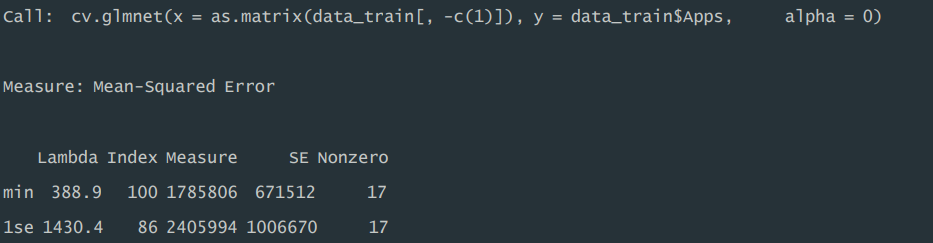
2）测试误差。根据运行结果显示，交叉验证的岭回归模型，在测试集表现中，RMSE 为 1108.10，MAE 为 605.30。

运行程序：

ridge_model <- glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps, alpha = 0, lambda = best_lambda)ridge_pred <- predict(ridge_model, newx = as.matrix(data_test[,-c(1)]), s = best_lambda)  ridge_error_RMSE=sqrt(mean((ridge_pred-data_test$Apps)^2)) #计算均方根误差
ridge_error_MAE=mean(abs(ridge_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证岭回归测试误差RMSE:",ridge_error_RMSE))
print(paste("交叉验证岭回归测试误差MAE:",ridge_error_MAE))

运行结果：

8 拟合LASSO模型

1）模型总结。训练集中，在拟合 LASSO 回归模型过程中，利用交叉验证的方式选择最优正则化λ，根据结果运行显示，对应最小 MSE 的λ值为 2.1，MSE 为 1346355，在该 λ 值下，模型中非零系数的数量为 17（不包含截距项），且在最小 MSE 的一个标准误差内的最大 λ 值为 346.2，MSE 为 1587747，该 λ 值下，模型中非零系数的数量为 2（不包含截距项）。

运行程序：

lasso_model=cv.glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps,alpha=1) #交叉验证拟合lasso回归模型
print(lasso_model) #输出模型

运行结果：

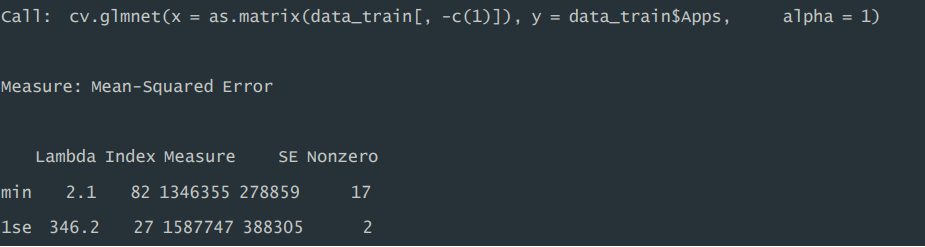
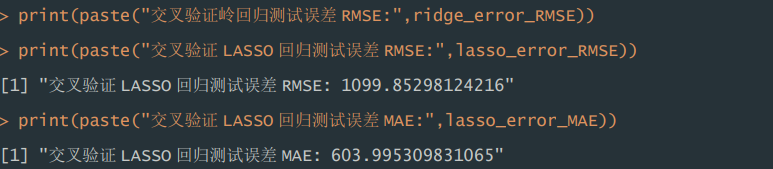
2）测试误差。根据运行结果显示，交叉验证的 LASSO 回归模型，在测试集表现中，RMSE 为 1099.85，MAE 为 604.00。

运行程序：

best_lambda <- lasso_model$lambda.min 
print(paste("最优lambda:",best_lambda))# 使用最佳λ在训练集上重新拟合模型  
lasso_model <- glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps, alpha = 1, lambda = best_lambda)
lasso_pred=predict(lasso_model,newx = as.matrix(data_test[,-c(1)]), s = best_lambda) #对测试集进行预测
lasso_error_RMSE=sqrt(mean((lasso_pred-data_test$Apps)^2)) #计算均方根误差
lasso_error_MAE=mean(abs(lasso_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证LASSO回归测试误差RMSE:",lasso_error_RMSE))
print(paste("交叉验证LASSO回归测试误差MAE:",lasso_error_MAE))

运行结果：

9 拟合 PCR 模型

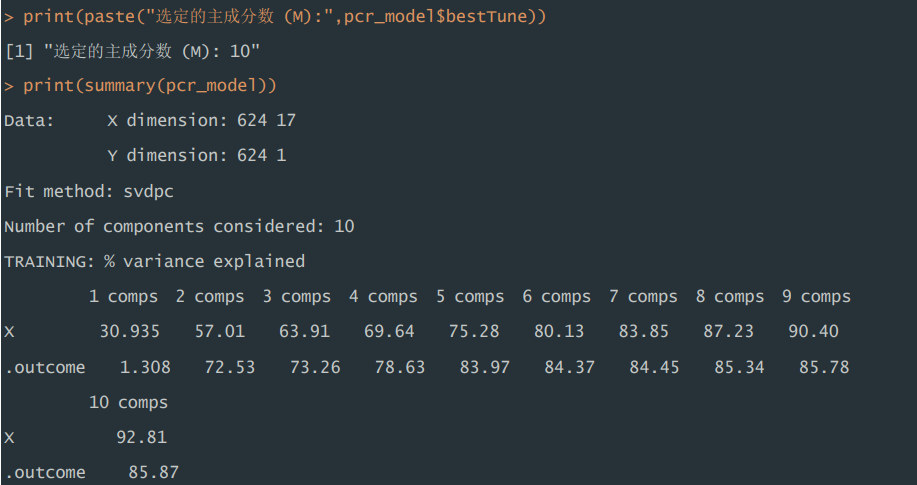
1）模型总结。训练集中，在拟合 PCR 模型过程中，利用交叉验证的方式选择最优主成分数量 M 为 10，当使用 10 个主成分时，可以解释原始数据中 85.87%的方差，解释能力较强。

运行程序：

##拟合PCR模型
pcr_model=train(Apps~.,data=data_train,method="pcr",preProcess=c("center","scale"),tuneLength=10) #交叉验证拟合主成分回归模型##选定的主成分数M
print(paste("选定的主成分数 (M):",pcr_model$bestTune))
print(summary(pcr_model))

运行结果：

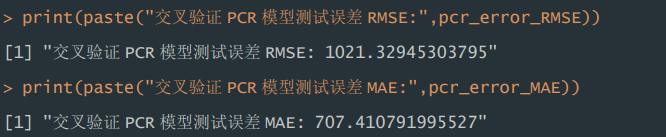
2）测试误差。根据运行结果显示，交叉验证的 PCR 模型，在测试集表现中，RMSE 为 1021.33，MAE 为 707.41。

运行程序：

pcr_pred=predict(pcr_model,newdata=data_test)pcr_error_RMSE=sqrt(mean((pcr_pred-data_test$Apps)^2)) #计算均方根误差
pcr_error_MAE=mean(abs(pcr_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证PCR模型测试误差RMSE:",pcr_error_RMSE))
print(paste("交叉验证PCR模型测试误差MAE:",pcr_error_MAE))

运行结果：

10 拟合PLS模型

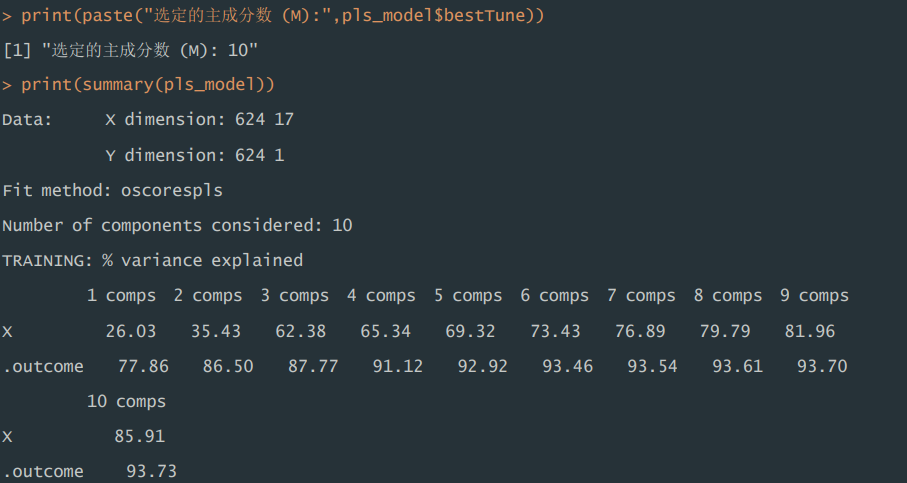
1）模型总结。训练集中，在拟合 PLS 回归模型过程中，利用交叉验证的方式选择最优主成分数量 M 为 10，当使用 10 个主成分时，可以解释原始数据中 93.73%的方差，解释能力较强。

运行程序：

pls_model=train(Apps~.,data=data_train,method="pls",preProcess=c("center","scale"),tuneLength=10) #交叉验证拟合偏最小二乘回归##选定的主成分数M
print(paste("选定的主成分数 (M):",pls_model$bestTune))
print(summary(pls_model))

运行结果：

2）测试误差。根据运行结果显示，交叉验证的 PCR 模型，在测试集表现中，RMSE 为 1095.97，MAE 为 607.09。

运行程序：

pls_pred=predict(pls_model,newdata=data_test)pls_error_RMSE=sqrt(mean((pls_pred-data_test$Apps)^2)) #计算均方根误差
pls_error_MAE=mean(abs(pls_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证PLS模型测试误差RMSE:",pls_error_RMSE))
print(paste("交叉验证PLS模型测试误差MAE:",pls_error_MAE))

运行结果：

11 模型评估

本实验在训练集过程中，利用训练集分别拟合了最小二乘线性回归模型、交叉验证的岭回归模型、交叉验证的 LASSO 模型、PCR 模型、PLS 回归模型五个模型，并在测试集进行测试，以 RMSE、MAE 指标评估模型。结果见表 1 所示。

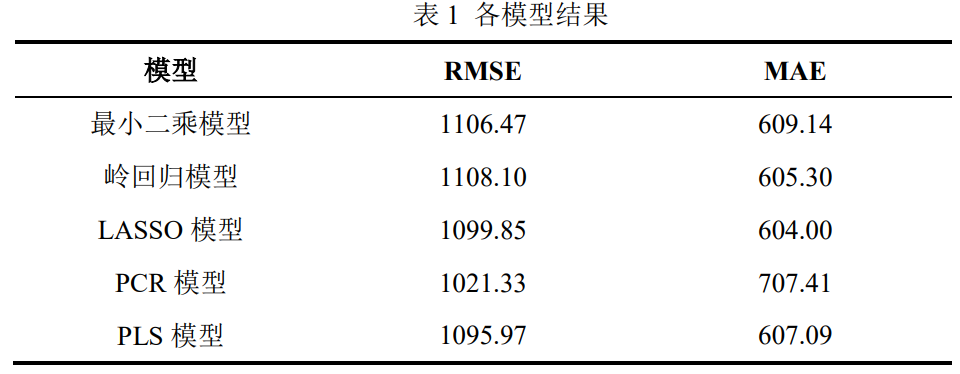
根据表 1 可以看出，五种模型在测试集表现中，RMSE 集中在 1100 附近，其中 PCR 模型的 RMSE 指标最低，MAE 大多集中在 600 附近，PCR 为 707，五种模型总体上性能相似。

12 完整代码

##加载相关包并读取数据
library("class")  
library("caret") 
library("gmodels") 
library('pls')
data<- read.csv("D:\\机器学习与R语言\\College.csv",header = T)
head(data)     #查看前六行str(data)                       #查看数据类型table(data$Private)
data$Private_Yes=ifelse(data$Private=="Yes",1,0) #将分类变量Private转化为0-1变量，保存为Private_Yes
data=data[c(1,3:20)]                            ##剔除字符变量Privatedata<-data[c('Apps','Accept','Enroll','Top10perc','Top25perc','F.Undergrad','P.Undergrad','Outstate','Room.Board','Books','Personal','PhD','Terminal','S.F.Ratio','perc.alumni','Expend','Grad.Rate','Private_Yes')]summary(data)set.seed(123) #设置随机种子以保证结果可重复
trainIndex=createDataPartition(data$Apps,p=0.8,list=FALSE,times=1)data_train<-data[trainIndex, ] #创建训练集
data_test<-data[-trainIndex, ] #创建测试集##最小二乘线性回归
lm_model=lm(Apps~.,data=data_train) #拟合线性回归模型
summary(lm_model)lm_pred=predict(lm_model,newdata=data_test) #对测试集进行预测
lm_error_RMSE=sqrt(mean((lm_pred-data_test$Apps)^2)) #计算均方根误差
lm_error_MAE=mean(abs(lm_pred-data_test$Apps)) #计算绝对平均误差print(paste("线性模型测试误差RMSE:",lm_error_RMSE))
print(paste("线性模型测试误差MAE:",lm_error_MAE))##拟合岭回归模型
ridge_model=cv.glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps,alpha=0) #交叉验证拟合岭回归模型
print(ridge_model) #输出模型# 使用最佳λ在训练集上重新拟合模型  
ridge_model <- glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps, alpha = 0, lambda = best_lambda)ridge_pred <- predict(ridge_model, newx = as.matrix(data_test[,-c(1)]), s = best_lambda)  ridge_error_RMSE=sqrt(mean((ridge_pred-data_test$Apps)^2)) #计算均方根误差
ridge_error_MAE=mean(abs(ridge_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证岭回归测试误差RMSE:",ridge_error_RMSE))
print(paste("交叉验证岭回归测试误差MAE:",ridge_error_MAE))##LASSO回归
lasso_model=cv.glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps,alpha=1) #交叉验证拟合lasso回归模型
print(lasso_model) #输出模型# 选择最佳λ（最小交叉验证误差的λ）  
best_lambda <- lasso_model$lambda.min 
print(paste("最优lambda:",best_lambda))# 使用最佳λ在训练集上重新拟合模型  
lasso_model <- glmnet(as.matrix(data_train[,-c(1)]),data_train$Apps, alpha = 1, lambda = best_lambda)
lasso_pred=predict(lasso_model,newx = as.matrix(data_test[,-c(1)]), s = best_lambda) #对测试集进行预测
lasso_error_RMSE=sqrt(mean((lasso_pred-data_test$Apps)^2)) #计算均方根误差
lasso_error_MAE=mean(abs(lasso_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证LASSO回归测试误差RMSE:",lasso_error_RMSE))
print(paste("交叉验证LASSO回归测试误差MAE:",lasso_error_MAE))##拟合PCR模型
pcr_model=train(Apps~.,data=data_train,method="pcr",preProcess=c("center","scale"),tuneLength=10) #交叉验证拟合主成分回归模型##选定的主成分数M
print(paste("选定的主成分数 (M):",pcr_model$bestTune))
print(summary(pcr_model))pcr_pred=predict(pcr_model,newdata=data_test)pcr_error_RMSE=sqrt(mean((pcr_pred-data_test$Apps)^2)) #计算均方根误差
pcr_error_MAE=mean(abs(pcr_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证PCR模型测试误差RMSE:",pcr_error_RMSE))
print(paste("交叉验证PCR模型测试误差MAE:",pcr_error_MAE))##拟合PLS回归模型
pls_model=train(Apps~.,data=data_train,method="pls",preProcess=c("center","scale"),tuneLength=10) #交叉验证拟合偏最小二乘回归##选定的主成分数M
print(paste("选定的主成分数 (M):",pls_model$bestTune))
print(summary(pls_model))pls_pred=predict(pls_model,newdata=data_test)pls_error_RMSE=sqrt(mean((pls_pred-data_test$Apps)^2)) #计算均方根误差
pls_error_MAE=mean(abs(pls_pred-data_test$Apps)) #计算绝对平均误差print(paste("交叉验证PLS模型测试误差RMSE:",pls_error_RMSE))
print(paste("交叉验证PLS模型测试误差MAE:",pls_error_MAE))